Contoh Soal Melakukan manipulasi aljabar dalam masalah menyelesaikan matematika dalam pertidaksamaan Mutlak
Contoh Soal Melakukan manipulasi aljabar dalam masalah menyelesaikan matematika dalam pertidaksamaan Mutlak - Senang bertemu kembali dengan adik-adik. Kali ini kita akan belajar tentang topik manipulasi aljabar dalam menyelesaikan pertidaksaman mutlak. Mari kita mulai belajar.
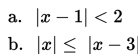
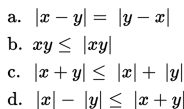
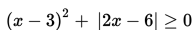
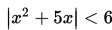
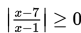
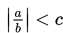
1. Pertidaksamaan Mutlak
Pertidaksamaan mutlak adalah pertidaksamaan yang melibatkan tanda mutlak. Berikut ini diberikan beberapa contoh pertidaksamaan mutlak:
Pertidaksamaan mutlak adalah pertidaksamaan yang melibatkan tanda mutlak. Berikut ini diberikan beberapa contoh pertidaksamaan mutlak:
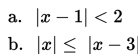
Beberapa sifat pertidaksamaan mutlak
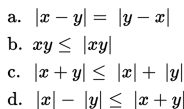
2. Bentuk dan Cara Menyelesaikan Pertidaksamaan Mutlak
Berikut ini beberapa bentuk dari pertidaksamaan mutlak.
a. | f(x) | < a dan a > 0
Bentuk ini dapat diselesaikan dengan bentuk –a < f(x) < a.
Bentuk ini dapat diselesaikan dengan bentuk –a < f(x) < a.
Contoh:
Tentukan himpunan penyelesaian dari pertidaksamaan |x – 4| < 3.
Tentukan himpunan penyelesaian dari pertidaksamaan |x – 4| < 3.
Penyelesaian:
Bentuk penyelesaian adalah
-3 < x – 4 < 3
Dengan manipulasi aljabar, diperoleh
-3 < x – 4 < 3
-3 + 4 < x < 3 + 4
1 < x < 7
Jadi, himpunan penyelesaian { x | 1 < x < 7 }
-3 < x – 4 < 3
Dengan manipulasi aljabar, diperoleh
-3 < x – 4 < 3
-3 + 4 < x < 3 + 4
1 < x < 7
Jadi, himpunan penyelesaian { x | 1 < x < 7 }
b. | f(x) | > a dan a > 0
Bentuk ini dapat diselesaikan dengan bentuk f(x) < -a.atau f(x) > a.
Bentuk ini dapat diselesaikan dengan bentuk f(x) < -a.atau f(x) > a.
Contoh:
Tentukan himpunan penyelesaian dari pertidaksamaan |x – 1| > 2 .
Tentukan himpunan penyelesaian dari pertidaksamaan |x – 1| > 2 .
Penyelesaian:
Bentuk penyelesaian adalah
x – 1 < -2 atau x – 1 > 2
x – 1 < -2 atau x – 1 > 2
Dengan manipulasi aljabar, diperoleh
x – 1 < -2 atau x – 1 > 2
x < -2 + 1 atau x > 2 + 1
x < -1 atau x > 3
x – 1 < -2 atau x – 1 > 2
x < -2 + 1 atau x > 2 + 1
x < -1 atau x > 3
Jadi, himpunan penyelesaian { x | x < -1 atau x > 3 }
c. | f(x) | > | g(x) |
Bentuk ini dapat diselesaikan dengan cara mengkuadratkan kedua ruas.
Bentuk ini dapat diselesaikan dengan cara mengkuadratkan kedua ruas.
Contoh:
Tentukan himpunan penyelesaian dari pertidaksamaan |x – 1| < |x – 2|.
Tentukan himpunan penyelesaian dari pertidaksamaan |x – 1| < |x – 2|.
Penyelesaian:
Kuadratkan kedua ruas sehingga diperoleh
|x – 1|2 < |x – 2|2
(x – 1)2 < (x – 2)^ 2
X2 – 2x + 1 < x2 – 4x + 4
|x – 1|2 < |x – 2|2
(x – 1)2 < (x – 2)^ 2
X2 – 2x + 1 < x2 – 4x + 4
Dengan manipulasi aljabar, diperoleh
x2 – 2x + 1 – (x2 – 4x + 4) < 0
2x – 3 < 0
2x < 3
x < 3/2
x2 – 2x + 1 – (x2 – 4x + 4) < 0
2x – 3 < 0
2x < 3
x < 3/2
Jadi, himpunan penyelesaian { x | x < 3/2 }
S1
Himpunan penyelesaian dari pertidaksamaan |x – 1| < 7 adalah....
S2
Himpunan penyelesaian dari pertidaksamaan |2x – 3| > 5 adalah....
S3
Himpunan penyelesaian dari pertidaksamaan |x – 3| < |x – 5| adalah...
S4
Himpunan penyelesaian yang memenuhi pertidaksamaan x < |x – 3| adalah...
S5
Himpunan penyelesaian pertidaksamaan
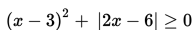
adalah ....
S6
Himpunan penyelesaian pertidaksamaan
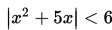
adalah ....
S7
Nilai dari
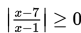
dipenuhi oleh ....
S8
Himpunan penyelesaian dari |x – 1| ≥ 1 adalah ....
S9
Pernyataan yang benar untuk himpunan penyelesaian dari pertidaksamaan a < |f(x)| < b, dengan a, b positif adalah...
S10
Pernyataan yang benar tentang manipulasi aljabar pertidaksamaan
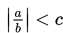
dengan c > 0 adalah....
