Contoh Soal Konsep Irisan Kerucut Ellips
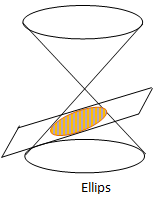
Contoh Soal Konsep Irisan Kerucut Ellips - Suatu kerucut tegak jika dipotong oleh bidang datar yang mengiris miring sisi tegak lengkung kerucut dengan sudut kemiringan antara 0o dan 45o maka irisannya akan menghasilkan suatu bentuk baru yang disebut ellips.

Persamaan Ellips dengan pusat di (0,0)
Ellips Horizontal
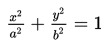
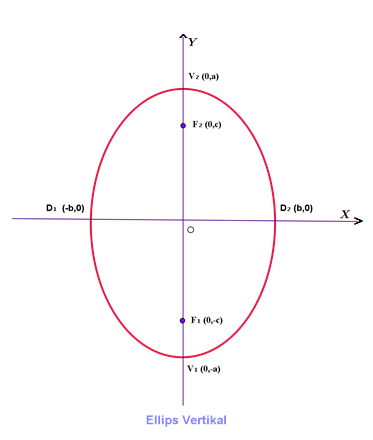
Ellips Vertikal
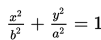
Persamaan Ellips dengan pusat di (p,q)

sehingga hubungan koordinat hasil translasi (x’,y’) dengan koordinat awal adalah
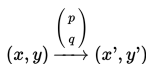
Dengan demikian,
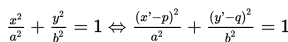
Selanjutnya, jika tanda aksen dihilangkan, maka akan kita peroleh persamaan ellips dengan pusat (p,q) sebagai berikut :
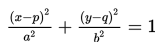
Ellips horizontal dengan pusat (p,q)
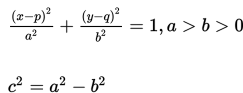
Ellips vertikal dengan pusat (p,q)

Contoh 1
Penyelesaian
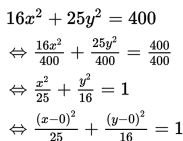
Contoh 2
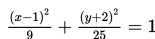
Penyelesaian :
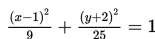
Jadi, koordinat titik fokusnya adalah (1 , 2) dan (1 , -6)
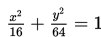
memiliki koordinat titik fokus pada ….
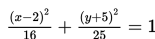
berturut-turut adalah…
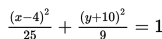
adalah…
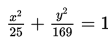
adalah…
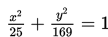
dengan sumbu Y adalah.…

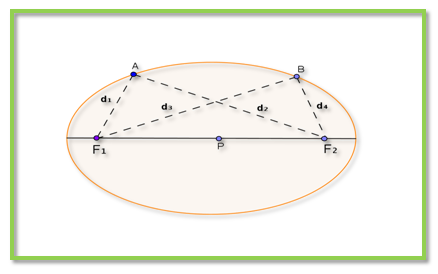
Ellips didefinisikan sebagai kedudukan titik-titik yang jumlah jaraknya dari dua titik tetap adalah konstan. Kedua titik tetap ini dinamakan fokus dari elips. Ambil dua titik pada ellips yaitu A dan B maka menurut definisi ellips AF1 + AF2 = BF1 + BF2 atau d1 + d2 = d3 + d4

Ellips dibedakan menjadi ellips horizontal dan ellips vertikal.
Ellips horizontal adalah ellips yang diameter horizontalnya lebih panjang dari pada diameter vertikalnya, sedangkan ellips vertikal adalah ellips yang diameter vertikalnya lebih panjang daripada diameter horizontalnya.
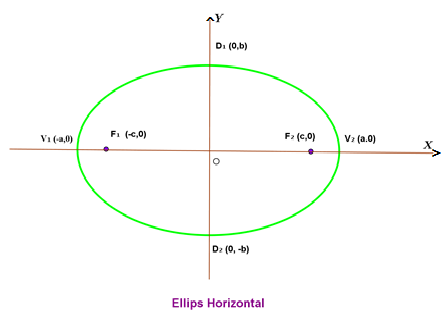
Pada gambar di bawah ini, diameter yang lebih panjang adalah V1V2 dan diameter yang lebih pendek adalah D1D2. Selanjutnya, V1V2 disebut sumbu mayor dan D1D2 disebut sumbu minor. Adapun dua titik yang terletak pada sumbu mayor, yaitu F1 dan F2nantinya akan disebut sebagai titik fokus .
Dengan demikian, dapat disimpulkan bahwa unsur-unsur ellips adalah : titik pusat, titik fokus, titik puncak, sumbu mayor (sumbu panjang) dan sumbu minor (sumbu pendek).

Persamaan Ellips dengan pusat di (0,0)
Ellips Horizontal

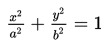
- Titik potong sumbu X = ±a
- Titik potong sumbu Y = ±b
- Fokus F1(-c,0) dan F2(c,0)
- Hubungan: c2 = a2 - b2
- Eksentrisitas: e = c/a, 0 < e < 1
- Panjang sumbu mayor = 2a
- Panjang sumbu minor = 2b
Ellips Vertikal

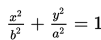
- Titik potong sumbu X = ±b
- Titik potong sumbu Y = ±a
- Fokus F1(0,c) dan F2(0,-c)
- Hubungan: c2 = a2 – b2
- Eksentrisitas: e = c/a, 0 < e < 1
- Panjang sumbu mayor = 2a
- Panjang sumbu minor = 2b
Persamaan Ellips dengan pusat di (p,q)
Persamaan ellips dengan pusat di (p,q) adalah sama dengan melakukan translasi pusat (0,0) dengan

sehingga hubungan koordinat hasil translasi (x’,y’) dengan koordinat awal adalah
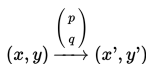
dimana x’ = x + p dan y’ = y + p
Dengan demikian,
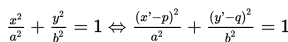
Selanjutnya, jika tanda aksen dihilangkan, maka akan kita peroleh persamaan ellips dengan pusat (p,q) sebagai berikut :
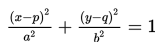
Ellips horizontal dengan pusat (p,q)
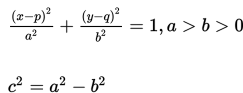
- Puncak horizontal : V1 = (p+a,q) dan V2 = (p-a,q)
- Puncak Vertikal : D1 = (p,q+b) dan D2 = (p,q-b)
- Fokus : F1 = (p+c,q) dan F2 = (p-c,q)
Ellips vertikal dengan pusat (p,q)

- Puncak horizontal : V1 = (p,q+a) dan V2 = (p,q-a)
- Puncak Vertikal : D1 = (p+b,q) dan D2 = (p-b,q)
- Fokus : F1 = (p,q+c) dan F2 = (p,q-c)
Contoh 1
Tentukan panjang sumbu mayor untuk ellips 16x2 +25y2 = 400
Penyelesaian
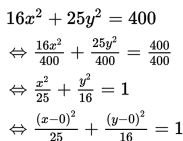
Dari persamaan di atas terlihat bahwa a2 = 25 <=> a = 5 (a > 0) dan b2 = 16 <=> b = 4 (b > 0). Dengan demikian, sumbu mayor untuk ellips 16x2 +25y2 = 400 adalah 10 satuan.
Contoh 2
Tentukan koordinat titik fokus untuk ellips di bawah ini!
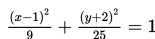
Penyelesaian :
Persamaan ellips yang berpusat di (1,-2) adalah :
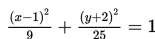
Dari persamaan di atas, diperoleh : a = 5, b = 3, dan c = 4.
Akibatnya, ellips yang terbentuk adalah ellips vertikal dengan fokus : F1 = (p , q+c) dan F2 = (p , q-c)
Akibatnya, ellips yang terbentuk adalah ellips vertikal dengan fokus : F1 = (p , q+c) dan F2 = (p , q-c)
Jadi, koordinat titik fokusnya adalah (1 , 2) dan (1 , -6)
S1
Jika suatu kerucut tegak diiris oleh bidang datar dengan sudut yang memiliki nilai sin ϴ = ½ maka irisannya akan berupa ....
S2
Jika suatu ellips memiliki persamaan 9x2 + 16y2 = 144 maka jenisnya adalah …
S3
Ellips dengan persamaan
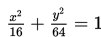
memiliki koordinat titik fokus pada ….
S4
Koordinat titik pusat dan koordinat fokus ellips
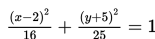
berturut-turut adalah…
S5
Koordinat titik puncak vertikal untuk ellips
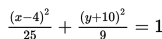
adalah…
S6
Suatu ellips berpusat di (0,0) memiliki fokus di (3,0) dan (-3,0) serta salah satu puncaknya di (-5,0) maka persamaan ellipsnya adalah... .
S7
Panjang sumbu minor pada persamaan ellips
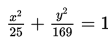
adalah…
S8
Ordinat titik potong antara ellips
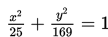
dengan sumbu Y adalah.…
S9
Titik-titik puncak ellips 9x2 + 25y2 = 900 berturut-turut adalah ….
S10
Koordinat titik pusat irisan kerucut 16x2 + 25y2 – 32x + 200y + 16 = 0 adalah ….
