Contoh Soal Komposisi Transformasi Menggunakan Matriks

Contoh Soal Komposisi Transformasi Menggunakan Matriks - Ketika kita belajar tentang komposisi transformasi, kita telah mengetahui hubungan antara urutan komposisi dan bayangan yang dihasilkan. Saat kita menggeser (translasi) suatu benda, kemudian memutar (rotasi) posisi benda tersebut pada suatu busur lingkaran, hasil akhir posisi benda yang kita peroleh belum tentu sama ketika kita memutar (rotasi) dahulu baru menggeser (translasi) posisi benda tersebut.

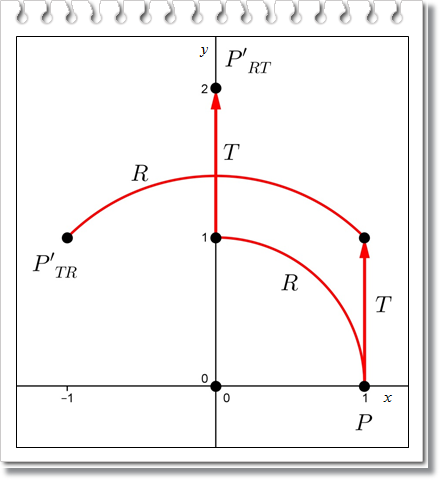
        Misalkan T1$T_1$, T2$T_2$, dan T3$T_3$ merupakan transformasi-transformasi geometri yang diterapkan secara berurutan terhadap objek geometri P. Urutan transformasi-transformasi tersebut akan sangat berpengaruh terhadap bayangan dari objek geometri P. Dengan kata lain, bayangan yang dihasilkan oleh komposisi transformasi T1∘T2∘T3$T_1\circ T_2\circ T_3$ belum tentu sama dengan bayangan yang dihasilkan oleh komposisi T3∘T2∘T1$T_3\circ T_2\circ T_1$. Mengapa demikian? Nah, untuk menjawab pertanyaan tersebut, kamu perlu mempelajari topik beikut, yaitu komposisi transformasi menggunakan matriks.

♔ KONSEP

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Pada topik sebelumnya, kita telah mengatahui peranan matriks dalam penentuan bayangan suatu objek geometri yang ditransformasikan. Sekarang , kita akan belajar menggunakan matriks tersebut untuk menghitung hasil transformasi secara efisien. Bagaimana caranya? Untuk memahaminya, mari simak dengan saksama.

𝓐. Matriks dalam transformasi
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅

Misalkan transformasi T memetakan titik P(a, b) ke titik P’(a’, b’). Apabila titik P’(a’, b’) dinyatakan sebagai kombinasi linear dari titik P(a, b), maka kita dapat menuliskan hubungan titik dan bayangannya sebagai berikut.

a′=ka+lbb′=ma+nb$\begin{array}{l}{a}^{\prime }=ka+lb\\ b^{\prime }=ma+nb\end{array}$

Dalam notasi matriks, ditulis:

        Agar kamu dapat dengan mudah memahami meteri ini, kamu harus mengingat kembali konsep-konsep transformasi yang telah kamu pelajari. Berikut ini adalah tabel matriks-matriks transformasi geometri yang telah kamu pelajari sebelumnya.

SOAL 1

Jika titik P secara berturut-turut ditransformasi oleh T1$T_1$, T2$T_2$, dan T3$T_3$, maka notasi komposisi transformasi yang sesuai adalah ….

SOAL 2

Lingkaran x2+y2=1$x^2+y^2=1$ ditransformasi secara berturut-turut oleh M1$M_1$, M2$M_2$, dan M3$M_3$. Apabila M1$M_1$ menyatakan dilatasi dengan faktor skala 2 terhadap titik asal, M2$M_2$ menyatakan refleksi terhadap garis y=2$y=2$, dan M3$M_3$ menyatakan rotasi sejauh 90° berlawanan arah putaran jarum jam terhadap titik asal, maka luas bayangan hasil komposisi transformasi lingkaran tersebut adalah ….

SOAL 3

Titik P(3, 1) mula-mula dicerminkan terhadap garis y=x$y=x$, kemudian didilatasi dengan faktor skala 5 terhadap titik asal. Bayangan akhir dari titik P(3, 1) adalah ….

SOAL 4

Jika titik P(3, 4) dirotasi sejauh 180° berlawanan arah putaran jarum jam dengan pusat titik asal, lalu direfleksi terhadap titik O(0, 0), maka bayangan akhir dari titik P(3, 4) adalah ….

SOAL 5

Refleksi terhadap garis y=x$y=x$, rotasi sejauh 45° berlawanan arah putaran jarum jam terhadap titik asal, dan dilatasi dengan faktor skala 22–√$2\sqrt{2}$diterapkan secara berurutan pada titik P(3, 7). Bayangan akhir dari titik P(3, 7) adalah ….

SOAL 6

Billy sedang berusaha membuat gambar lingkaran yang cocok untuk desain suatu logo perusahaan dengan menggunakan software penggambar. Secara berturut-turut, Billy memperbesar dan memperkecil ukuran lingkaran awal dengan faktor skala 3, 12$\frac{1}{2}$, 14$\frac{1}{4}$, dan 6. Akhirnya, Billy puas dengan lingkaran akhir yang ia peroleh. Apabila persamaan awal lingkaran adalah x2+y2=1$x^2+y^2=1$, maka persamaan lingkaran akhir yang digunakan Billy sebagai logo adalah ….

SOAL 7

Garis y=2x−1$y=2x-1$ mula-mula dicerminkan terhadap garis y=−x$y=-x$, kemudian dilanjutkan dengan pencerminan terhadap garis y=x$y=x$. Bayangan yang dihasilkan dari kedua pencerminan tersebut adalah ….

SOAL 8

Parabola y=x2+2$y=x^2+2$ mula-mula dicerminkan terhadap sumbu-x$x$, kemudian dirotasi sejauh 90° berlawanan arah jarum jam terhadap titik asal, dan terakhir didilatasi dengan faktor skala 2 terhadap titik asal. Bayangan yang dihasilkan dari komposisi transformasi tersebut adalah …

SOAL 9

Diketahui koordinat titik-titik sudut persegi ABCD adalah A(2, 2), B(2, -2), C(-2, -2), dan D(-2, 2). Jika persegi ABCD mula-mula dicerminkan terhadap garis y=x$y=x$, kemudian dilanjutkan dengan rotasi sejauh 90° searah putaran jarum jam terhadap titik asal, dan diakhiri dengan dilatasi dengan faktor skala 3 terhadap titik asal, maka koordinat bayangan akhir titik-titik sudut persegi ABCD tersebut adalah ….

SOAL 10

Diberikan dua matriks transformasi berikut.

M1=[−abba]M2=[abb−a]$M_1=\left[\begin{array}{ll}-a& b\\ b& a\end{array}\right]\begin{array}{ll}& M_2=\left[\begin{array}{ll}a& b\\ b& -a\end{array}\right]\end{array}$

Kedua matriks tersebut masing-masing mewakili transformasi T1$T_1$ dan T2$T_2$. Matriks transformasi yang bersesuaian dengan komposisi transformasi T2∘T1$T_2\circ T_1$ adalah:

M3=[−100−1]$M_3=\left[\begin{array}{ll}-1& 0\\ 0& -1\end{array}\right]$

Jika a$a$ dan b$b$ bilangan bulat, maka komponen dari matriks transformasi M1$M_1$ adalah ….

Share this post