Menghitung Limit Fungsi Aljabar Berbentuk limit f(x) x->a, a≠0

Menghitung Limit Fungsi Aljabar Berbentuk limit f(x) x->a, a≠0 - Pada topik-topik sebelumnya, kalian telah belajar mengenai teorema dasar limit. Apakah kalian masih ingat? 

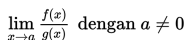
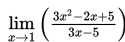
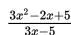
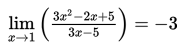
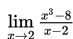
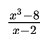
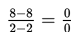
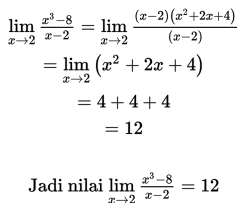
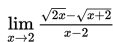
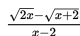
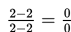
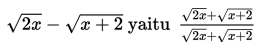
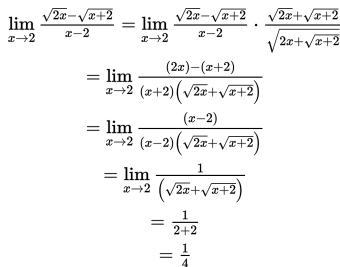
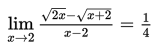
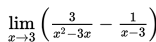
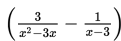
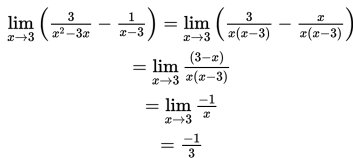
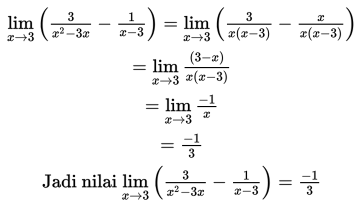
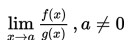
Menghitung Limit Fungsi Aljabar Berbentuk limit f(x) x->a, a≠0

Dalam topik ini kalian akan belajar tentang bagaimana menghitung limit fungsi aljabar berbentuk

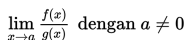
Untuk memperdalam pemahaman kalian, mari kita langsung belajar dari contoh.

• Hitung nilai

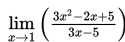
Penyelesaian:

Dengan cara subtitusi langsung x = 1 pada

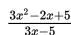
maka akan kita peroleh

Jadi nilai

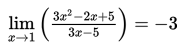
• Hitung nilai

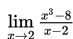
Penyelesaian:

Jika kita selesaikan dengan cara subtitusi langsung x = 2 pada

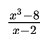
maka akan kita peroleh

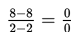
(tak didefinisikan), maka harus diselesaikan dengan cara lain yaitu dengan difaktorkan atau diuraikan terlebih dahulu, seperti kita lihat dan cermati berikut:

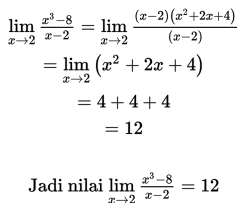
• Hitung nilai

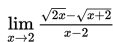
Penyelesaian:

Jika kita selesaikan dengan cara subtitusi langsung x = 2 pada

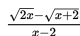
akan kita peroleh

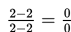
(tak didefinisikan), maka harus kita selesaikan dengan cara lain yaitu dikalikan dengan sekawan dari

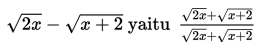
kemudian kita faktorkan terlebih dahulu, seperti kita lihat berikut:

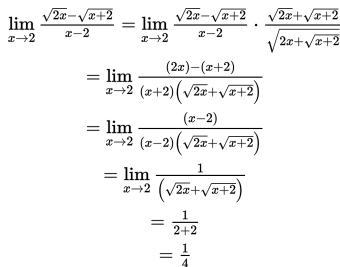
Jadi nilai

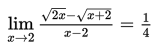
• Contoh yang lain, hitung nilai

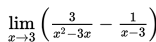
Penyelesaian:

Jika pada

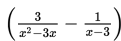
ini kita subtitusi langsung dengan x = 3 maka akan diperoleh 3/0 – 1/0 yang ini akan sama dengan ∞ - ∞. Oleh karena itu maka harus disederhanakan terlebih dahulu dengan menyamakan penyebutnya, seperti yang berikut:

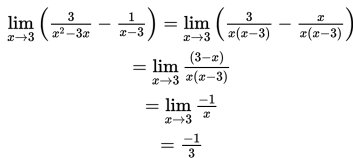
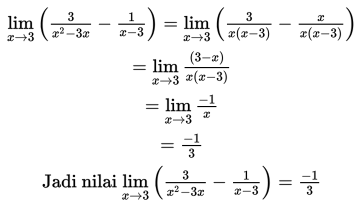
Dari contoh-contoh tersebut bisa kita lihat bahwa cara menyelesaikan limit fungsi aljabar berbentuk

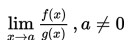
bisa dilakukan dengan beberapa cara antara lain dengan cara subtitusi langsung. Apabila dengan cara subtitusi langsung kita dapatkan bentuk tak tentu 0/0 atau ∞ - ∞ atau ∞ + ∞: apa yang harus kita lakukan? Jika kita peroleh 0/0, maka f(x) / g(x) harus difaktorkan terlebih dahulu atau diuraikan, dan jika diperoleh ∞ - ∞ dan ∞ + ∞ maka f(x) / g(x) harus disederhanakan terlebih dahulu dengan cara mengalikan bentuk sekawannya agar sifat-sifat limit fungsi dapat dipergunakan.

Share this post