Konsep Barisan pada Perhitungan Bunga Tunggal

Konsep Barisan pada Perhitungan Bunga Tunggal - Masih ingatkah kalian tentang bunga tunggal yang pernah kalian pelajari pada topik sebelumnya?

Konsep Barisan pada Perhitungan Bunga Tunggal

Ya, bunga tunggal adalah bunga yang diperoleh pada setiap akhir periode waktu tertentu dan besarnya tetap.

Dengan kata lain, perhitungan bunga untuk setiap periode selalu dihitung berdasarkan besar modal yang tetap, yaitu: bunga = modal ×$\times$ suku bunga tiap periode ×$\times$ banyak periode

Nah, tahukah kalian bahwa perhitungan bunga tunggal berkaitan erat dengan konsep barisan aritmetika?

Yuk kita cari tahu bagaimana penggunaan konsep barisan aritmetika pada perhitungan bunga tunggal.

Bunga Tunggal

Bu Tatyana menyimpan uang sebesar Rp1.000.000,00 di Bank. 
Diketahui bahwa Bank memberikan suku bunga tunggal sebesar 2% setiap bulannya.

Dapatkah kalian membantu bu Tatyana untuk menentukan besarnya bunga tunggal yang ia peroleh setelah 1 bulan, 2 bulan, 3 bulan, dan n bulan menabung?

Ya, tentu saja kalian dapat.

• Setelah 1 bulan, besar bunga adalah 2% ×$\times$ 1 ×$\times$ Rp1.000.000,00 = Rp20.000,00.
• Setelah 2 bulan, besar bunga adalah 2% ×$\times$ 2 ×$\times$ Rp1.000.000,00 = Rp40.000,00.
• Setelah 3 bulan, besar bunga adalah 2% ×$\times$ 3 ×$\times$ Rp1.000.000,00 = Rp60.000,00.

Berdasarkan pola pada uraian di atas, dapat kita simpulkan bahwa setelah n$n$ bulan, besar bunga adalah 2% ×n$\times n$ ×$\times$ Rp1.000.000,00 = n×$n\times$ Rp20.000,00.

Dengan demikian, besarnya bunga setiap bulan adalah sebagai berikut:

20.000, 40.000, 60.000, …

Apa yang dapat kalian simpulkan dari pola bilangan di atas?

Benar, pada pola bilangan di atas, selisih antara dua suku yang berurutan adalah sama, yaitu Rp20.000,00. Dengan kata lain, bunga tunggal membentuk barisan aritmetika.

Suku pertama dari barisan aritmetika ini adalah tabungan awal (M$M$), beda antar suku adalah besar bunga tunggal pada periode pertama, dan suku ke-n$n$ adalah tabungan akhir (Mn$M_n$).

Ingat, jika bunga pada periode pertama adalah a$a$, maka besarnya bunga pada periode ke-n$n$ adalah na$na$.

Tabungan Akhir

Apakah kalian masih ingat bagaimana cara menentukan besar tabungan akhir dengan bunga tunggal?

Ya, tabungan akhir = tabungan awal + bunga.

Mari kita kembali pada permasalahan bu Tatyana. 
Kali ini kita akan menjabarkan besar tabungan beliau setelah 1 bulan, 2 bulan, dan 3 bulan.

- Setelah 1 bulan, besar tabungan adalah Rp1.000.000,00 + Rp20.000,00 = Rp1020.000.000,00.
- Setelah 2 bulan, besar tabungan adalah Rp1.000.000,00 + Rp40.000,00 = Rp1.040.000.000,00.
- Setelah 3 bulan, besar tabungan adalah Rp1.000.000,00 + Rp60.000,00 = Rp1.060.000.000,00.

Berdasarkan uraian di atas, kita peroleh pola bilangan berikut:
1020.000.000, 1.040.000.000, 1.060.000.000, ...

Berdasarkan pola bilangan di atas, tampak bahwa selisih antara dua suku yang berurutan adalah sama, yaitu Rp20.000,00.

Nah, apa yang dapat kalian simpulkan?

Ya, besar tabungan akhir dengan suku bunga tunggal ternyata juga membentuk barisan aritmetika.

Agar kalian lebih paham dengan materi ini, mari kita perhatikan contoh berikut.

Contoh

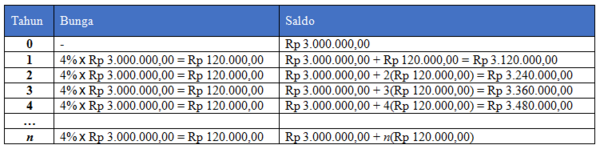
Denok menabung di koperasi pegawai yang memberikan bunga tunggal sebesar 4% per tahun. Jika Denok menabung sebesar Rp3.000.000,00, maka hitunglah uang Denok

1. pada akhir tahun ke-4
2. pada akhir tahun ke-12
3. pada akhir tahun ke-n$n$

Penyelesaian:

Berdasarkan tabel di atas, uang Denok pada akhir tahun ke-4 adalah Rp3.480.000,00.

Selanjutnya dengan melihat pola bilangan pada kolom saldo, dapat kita simpulkan bahwa besar uang Denok pada akhir tahun ke-12 adalah

Rp3.000.000,00+12×Rp120.000,00=Rp4.440.000,00$Rp\mathrm{3.000.000},00$

$+12\times Rp120.000,00=Rp\mathrm{4.440.000},00$

Adapun besar uang Denok pada akhir tahun ke-n$n$, berdasarkan pola bilangan pada kolom saldo adalah

Rp3.000.000,00+n×Rp120.000,00$Rp\mathrm{3.000.000},00+n\times Rp120.000,00$ .

Rumus

Besar tabungan pada akhir periode ke-n$n$ adalah Mn=M+nI$M_n=M+nI$, dengan

• M$M$ adalah besar tabungan awal
• n$n$ adalah banyak periode
• I$I$ adalah besarnya bunga

Perlu kalian ketahui, It=Mrt$I_t=Mrt$ adalah besar bunga setelah t$t$ periode.

Yuk kerjakan sepuluh latihan soal dalam topik ini untuk menguji pemahaman kalian.

Share this post