Aturan Penjumlahan
Aturan Penjumlahan - Kamu telah mempelajari nilai probabilitas dalam kisaran 0 sampai 1. Sebagai contoh, sebuah dadu bersisi 6 dilemparkan dan probabilitas dari pelemparan sebuah angka adalah 0.5 atau P(A) = 0.5. Bagaimana nilai penjumlahan probabilitasnya? Nilai makasimum adalah 1.
 |
| Aturan Penjumlahan |
Kali ini, kamu akan belajar mengenai
- Penggunaan aturan penjumlahan dalam probabilitas
- Menentukan kejadian saling lepas atau tidak saling lepas
Ingat bahwa P(A atau B) = P(AUB) dan P(A dan B) = P(A∩B).
Aturan penjumlahan untuk probabilitas didefinisikan sebagai berikut "Probabilitas kejadian A atau kejadian B sama dengan penjumlahan probabilitas kejadian A dan B dikurangi probabilitas kejadian A dan B yang sama"
Jadi, dalam pernyataan matematika dapat di tulis sebagai berikut:
P(A∪B) = P(A) + P(B) - P(A∩B)
Jika dua kejadian tidak terjadi pada waktu yang sama, maka dua kejadian tersebut disebut "kejadian saling lepas".Dengan kata lain, kejadian-kejadian itu saling lepas jika mereka tidak memiliki hasil yang sama. Karena kejadian A dan B saling lepas, jadi P(A∩B) = 0
Masukkan nilai itu ke dalam aturan penjumlahan:
P(AUB) = P(A) + P(B) - P(A∩B)
P(AUB) = P(A) + P(B) + 0
P(AUB) = P(A) + P(B)
Jika dua kejadian terjadi pada waktu yang sama, maka kejadian itu disebut "kejadian tidak saling lepas". Karena kejadian A dan B tidak saling lepas, jadi P(A∩B) ≠ 0
P(A∪B) = P(A) + P(B) - P(A∩B)
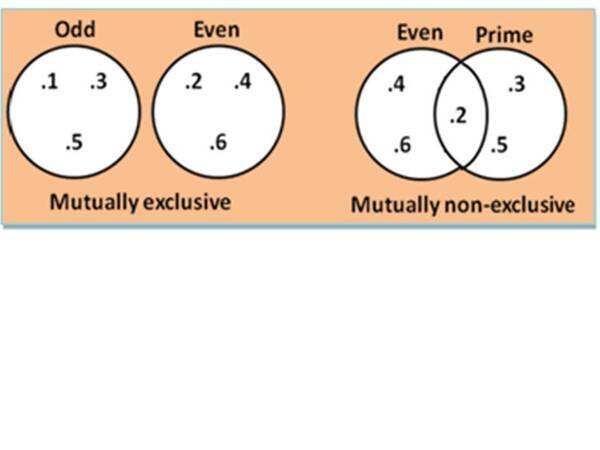
Contoh ini dapat menunjukkan perbedaan antara kejadian saling lepas dan kejadian tidak saling lepas. Ketika sebuah dadu bersisi 6 dilemparkan, anggap bahwa A adalah himpunan bilangan ganjil, B adalah himpunan bilangan genap, dan C adalah himpunan bilangan prima. Kita dapat melihat bahwa kejadian A dan B saling lepas tetapi kejadian B dan C tidak saling lepas.
Perhatikan gambar berikut :
Contoh 1
Diberikan P(A) = 0.6 dan P(B) = 0.2.Jika kejadian A dan B saling lepas, nilai dari P(A∪B) adalah
a. 0.4
b. 0.6
c. 0.8
d. 1
Penjelasan,
Karena kejadian A dan B saling lepas, jadi P(A∩B) = 0.
P(AUB) = P(A) + P(B) = 0.6 + 0.2 = 0.8
Jawabannya adalah C.
Contoh 2
Diberikan P(E) = 0.7, P(E∩F) = 0.4, dan P(EUF) = 0.8. Berapa nilai P(F)?
a. 0.1
b. 0.2
c. 0.4
d. 0.5
Penjelasan,
Masukkan nilai-nilai yang ada ke dalam aturan penjumlahan:
P(EUF) = P(E) + P(F) - P(E∩F)
0.8 = 0.7 + P(F) - 0.4
0.8 = 0.3 + P(F)
P(F) = 0.8 - 0.3 = 0.5
Jawabannya adalah D.
Contoh 3
Diberikan P(R) = 0.3, P(S) = 0.4, dan P(RUS) = 0.7. Tentukan apakah kejadian A dan B saling lepas atau tidak saling lepas.
Penjelasan,
Masukkan nilai-nilai yang ada ke dalam aturan penjumlahan:
P(RUS) = P(R) + P(S) - P(R∩S)
0.7 = 0.3 + 0.4 - P(R∩S)
0.7 = 0.7 - P(R∩S)
P(R∩S)= 0.7 - 0.7 = 0
Karena P(R∩S)=0, kejadian A dan B saling lepas.
