Contoh Soal Ukuran Penyebaran Data

Contoh Soal Ukuran Penyebaran Data - Untuk menghitung pemerataan usia penduduk, Badan Pusat Statistik (BPS) melakukan pendataan usia penduduk pada setiap kampung di sebuah kecamatan. Ternyata, diperoleh data yang menggambarkan bahwa kampung A memiliki rata-rata usia penduduk 35 tahun dengan usia termuda 5 tahun dan usia tertua 40 tahun. Penduduk di kampung B juga memiliki rata-rata usia 35 tahun dengan usia termuda 1 tahun dan usia tertua 65 tahun.

        Berdasarkan data yang diperoleh, dapat disimpulkan bahwa, meskipun kedua data memiliki rata-rata yang sama, belum tentu penyebaran datanya akan seragam. Oleh karena itu, kita perlu memahami penyebaran masing-masing datum dalam sebuah data dengan mempelajari ukuran penyebaran data.

       Ukuran penyebaran data merupakan pengolahan data yang menggambarkan keberagaman datum-datum dalam suatu data. Ada beberapa macam ukuran penyebaran data yang akan dipelajari pada topik ini, antara lain jangkauan, kuartil, jangkauan interkuarti, dan simpangan kuartil.

Jangkauan

Ukuran penyebaran data yang pertama adalah jangkauan. Apakah yang dimaksud dengan jangkauan suatu data? Jangkauan suatu data adalah selisih antara datum tertinggi dan datum terendah. Misalkan jangkauan dilambangkan dengan J, datum tertinggi dilambangkan dengan xmax, dan datum terendah dilambangkan dengan xmin, sehingga diperoleh rumus:

$J=x_{max}-x_{min}$

◙ ◙ ◙ Contoh 1 ◙ ◙ ◙

Diketahui tinggi badan siswa laki-laki kelas IX C sebagai berikut.
165, 160, 155, 170, 183, 160, 161, 162, 163, 163, 170.
Tentukan jangkauan dari data di atas.

Penyelesaian:

Untuk menentukan jangkauan, urutkan data tersebut dari yang terendah ke yang tinggi.

155, 160, 160, 161, 162, 163, 163, 165, 170, 170, 183.

Setelah diurutkan, ternyata datum tertinggi adalah 183 dan datum terendah adalah 155, sehingga:

$J=x_{max}-x_{min}$

$\iff J=183-155=28$

Kuartil

Pada topik sebelumnya, kita telah membahas mengenai median yang membagi data yang sudah diurutkan menjadi dua kelompok yang sama banyak. Bagaimana jika data yang telah terurut dibagi menjadi empat kelompok yang sama banyak? Jika data dibagi dengan cara demikian, maka akan diperoleh empat kelompok yang masing-masingnya terdiri atas $\frac{1}{4}$ data. Ukuran yang membagi data menjadi empat kelompok yang sama banyak disebut kuartil.

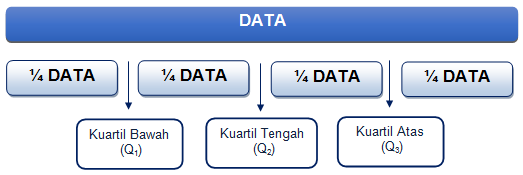
Dalam suatu data ada tiga jenis kuartil, yaitu kuartil bawah, kuartil tengah, dan kuartil atas. Untuk lebih jelasnya, perhatikan ilustrasi di bawah ini.

Misalkan suatu data digambarkan seperti berikut ini. Data tersebut dibagi menjadi empat bagian yang sama besar, sehingga menjadi:

Langkah-langkah untuk menentukan kuartil dari suatu data adalah sebagai berikut.

• Urutkan data dari yang terendah ke yang tertinggi.
• Tentukan median (Q2) dari data tersebut.
• Tentukan kuartil bawah (Q1) dengan membagi data di bawah median (Q2) menjadi dua bagian sama banyak.
• Tentukan kuartil atas (Q3) dengan cara membagi data di atas median (Q2) menjadi dua bagian sama banyak.

◙ ◙ ◙ Contoh 2 ◙ ◙ ◙

Diketahui hasil pengukuran berat badan beberapa orang siswa (dalam kilogram) adalah sebagai berikut.
45, 56, 60, 68, 72, 78, 80, 54, 53, 52.

Tentukan:

• kuartil bawah
• kuartil tengah (median)
• kuartil atas

Penyelesaian:

Untuk menentukan kuartil suatu data, urutkan data dari yang terendah ke yang tertinggi.

45, 52, 53, 54, 56, 60, 68, 72, 78, 80.

Tentukan median (kuartil tengah) terlebih dahulu.

Kuartil tengah (median) $=\frac{56+60}{2}=\frac{116}{2}=58$

Setelah memperoleh nilai median, bagi data di bawah median menjadi dua bagian yang sama besar sehingga diperoleh kuartil bawah (Q1).

Ini berarti, kuartil bawah (Q1) = 53.

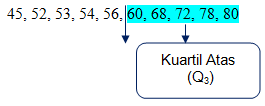
Selanjutnya, bagi data di atas median menjadi dua bagian yang sama besar, sehingga diperoleh kuarti atas (Q3).

Ini berarti, kuartil atas (Q3) = 72.

Bagaimana cara menentukan kuartil dari data yang disajikan dalam bentuk tabel distribusi frekuensi? Kuartil tersebut dapat ditentukan dengan rumus sebagai berikut.

Kuartil bawah $(Q_1)=x_{\frac{n+1}{4}}$

Kuartil tengah $(Q_2)=x_{\frac{2(n+1)}{4}}$

Kuartil atas $(Q_3)=x_{\frac{3(n+1)}{4}}$

dengan:
$x_{\frac{n+1}{4}}$ = data ke-$\frac{n+1}{4}$
$x_{\frac{2(n+1)}{4}}$ = data ke-$\frac{2(n+1)}{4}$
$x_{\frac{3(n+1)}{4}}$ = data ke-$\frac{3(n+1)}{4}$

Jika didapatkan hasil pecahan misalnya x7,5 berarti kuartilnya merupakan rata-rata dari x7 dan x8 yaitu $\left(\frac{x_7+x_8}{2}\right)$.

Jangkauan Interkuartil

Jangkauan interkuartil merupakan selisih antara kuartil atas dan kuartil bawah dari suatu data. Jika jangkauan interkuartil dinotasikan QR, maka diperoleh persamaan:

$Q_R=Q_3-Q_1$

Simpangan Kuartil

Simpangan kuartil (jangkauan semiinterkuartil) adalah setengah dari jangkauan interkuartil. Jika jangkauan semiinterkuartil dinotasikan dengan $Q_D$, maka diperoleh persamaan:

$Q_D=\frac{1}{2}{Q}_R=\frac{1}{2}(Q_3-Q_1)$

$<br>$

$<br>$

$<br>$

$<br>$

S1

$ Diketahui berat badan pemain Timnas Futsal Indonesia (dalam kg) adalah sebagai berikut. 65, 78, 82, 65, 51, 54, 52, 56, 67, 56, 51 Jangkauan dari data di atas adalah .... S2 Diketahui nilai 10 besar dari UAN Matematika SMP Sukses Selalu sebagai berikut. 85, p, 65, 75, 83, 80, 95, 100, 100, 95 Jika diketahui nilai tertinggi adalah 100 dan jangkauan datanya adalah 35, maka nilai p yang tidak memenuhi adalah .... S3 Suatu data diketahui memiliki jangkauan p. Jika seluruh datum pada data tersebut dikalikan dengan 2, maka jangkauan data tersebut akan menjadi .... S4 Diketahui hasil pengukuran berat badan beberapa orang siswa (dalam kilogram) adalah sebagai berikut. 45, 56, 60, 68, 72, 78, 80, 54, 53, 55, 55, 52 Kuartil bawah dan kuartil atas dari data di atas masing-masing adalah .... S5 Nilai ulangan Matematika dari suatu kelas adalah sebagai berikut. Kuartil bawah dari data di atas adalah .... S6 Nilai kuis Matematika dari suatu kelas disajikan dalam tabel berikut. Kuartil atas dari data di atas adalah .... S7 Diketahui suatu data memiliki kuartil bawah (Q1) = 45 dan kuartil atas (Q3) = 95. Jangkauan interkuartil dan simpangan kuartil dari data tersebut adalah .... S8 Diketahui hasil pengukuran tinggi badan beberapa orang siswa (dalam cm) adalah sebagai berikut. 146, 156, 160, 167, 172, 178, 180, 154, 153, 155,155,152 Jangkauan interkuartil dari data di atas adalah .... S9 Nilai kuis Matematika di suatu kelas adalah sebagai berikut. Simpangan kuartil dari data di atas adalah .... S10 Jika diketahui suatu data memiliki jangkauan = J, jangkauan interkuartil = QR, dan simpangan kuartil = QD, maka pernyataan yang benar di bawah ini adalah .... $

Share this post