Contoh Soal Perkalian dan Pembagian Aljabar
Contoh Soal Perkalian dan Pembagian Aljabar - Perhatikan gambar di bawah ini.
Perkalian Bilangan dengan Suku Tiga
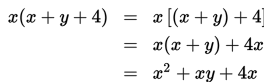
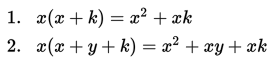
Perkalian suku dua dengan suku dua
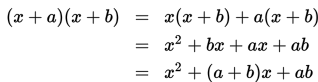
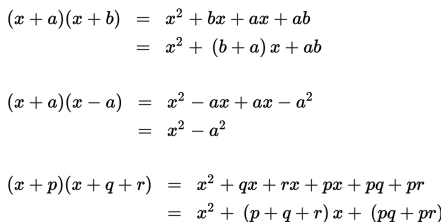
Contoh 1 :
Penyelesaian :
Contoh 2 :
Penyelesaian :
Contoh 3 :
Penyelesaian :
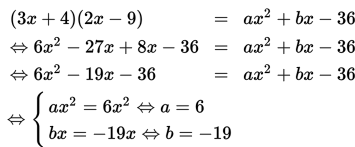
Contoh 4 :
Penyelesaian :
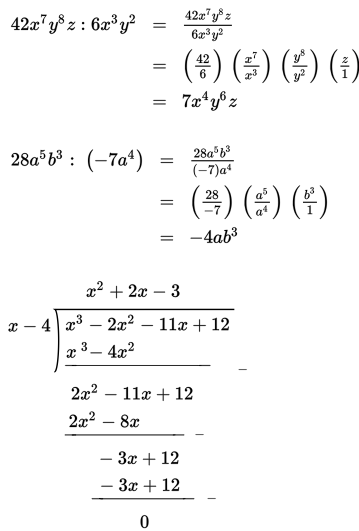
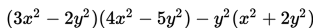

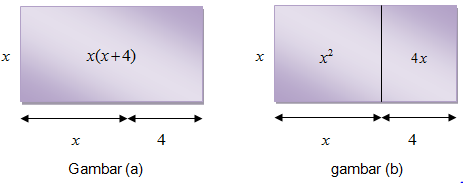
Gambar (a) menunjukkan sebuah persegi panjang dengan ukuran sebagai berikut :
• Panjang = (x + 4) satuan
• Lebar = x satuan
• Panjang = (x + 4) satuan
• Lebar = x satuan
Dengan demikian, luas persegi panjang tersebut = x(x + 4) satuan luas.
Gambar (b) menunjukkan bahwa untuk menentukan luas persegi panjang pada gambar (a), dapat dilakukan dengan cara membagi (menyekat) persegi panjang tersebut menjadi dua buah persegi panjang, sehingga luasnya menjadi x(x + 4).
Selanjutnya, karena luas kedua persegi panjang pada gambar (b) adalah sama, maka
x(x + 4) = x2 + 4x
x(x + 4) = x2 + 4x
Dengan demikian, bentuk perkalian x(x + 4) dapat dinyatakan sebagai bentuk penjumlahan x2 + 4x.
Perkalian Bilangan dengan Suku Tiga
Apabila digunakan cara seperti di atas, maka hasil perkalian suatu bilangan dengan suku tiga dapat ditentukan sebagai berikut :
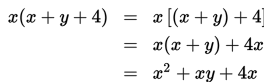
Perlu diketahui bahwa menyatakan bentuk perkalian menjadi bentuk penjumlahan pada bentuk aljabar disebut menjabarkan dan untuk sembarang bilangan x, y, dan k berlaku :
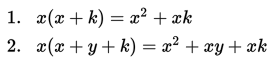
Perkalian suku dua dengan suku dua
Menggunakan hukum distributif
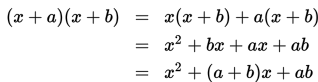
Menggunakan cara skema
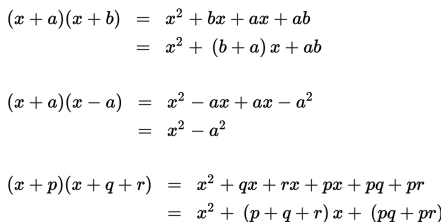
Sifat-sifat operasi perkalian bentuk aljabar
- Sifat komutatif : a X b = b X a
- Sifat asosiatif : a X (b X c) = (a X b) X c
- Sifat distributif : a X (b + c) = (a X b) + (a X c)
Pembagian Bentuk Aljabar
Jika dua bentuk aljabar memiliki faktor-faktor yang sama, maka hasil pembagian kedua bentuk aljabar tersebut dapat dinyatakan dalam bentuk yang sederhana dengan memperhatikan faktor-faktor yang sama.
Mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
Tentukan hasil kali dari bentuk-bentuk aljabar berikut!
- 10(2y – 10)
- (x + 5)(5x – 1)
- (2x + 3)(x2 + 2x – 5)
Penyelesaian :
10( 2y – 10)
= 10(2y) – 10(10)
= 20y - 100
= 10(2y) – 10(10)
= 20y - 100
(x + 5)(5x – 1)
= x(5x – 1) + 5(5x – 1)
= 5x2 – x + 25x – 5
= 5x2 + 24x – 5
= x(5x – 1) + 5(5x – 1)
= 5x2 – x + 25x – 5
= 5x2 + 24x – 5
(2x + 3)(x2 + 2x – 5)
= 2x(x2 + 2x – 5) + 3(x2 + 2x – 5)
= 2x3 + 4x2 – 10x + 3x2 + 6x – 15
= 2x3 + 7x2 – 4x – 15
= 2x(x2 + 2x – 5) + 3(x2 + 2x – 5)
= 2x3 + 4x2 – 10x + 3x2 + 6x – 15
= 2x3 + 7x2 – 4x – 15
Contoh 2 :
Jabarkan bentuk-bentuk berikut!
- 2x(4x2 – 3y)
- 4x(x2 + 2xy – 3y2)
Penyelesaian :
1. 2x(4x2 – 3y) = 8x3 – 6xy
2. 4x(x2 + 2xy – 3y2) = 4x3 + 8 x2y – 12xy2
Contoh 3 :
Tentukan nilai a dan b dari bentuk berikut :
(3x + 4)(2x – 9) = ax2 + bx - 36
(3x + 4)(2x – 9) = ax2 + bx - 36
Penyelesaian :
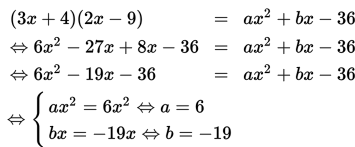
Contoh 4 :
Tentukan hasil pembagian bentuk aljabar berikut!
- 42x7y8z : 63y2
- 28a5b3 : (–7a4)
- (x3 – 2x2 – 11x + 12) : (x – 4)
Penyelesaian :
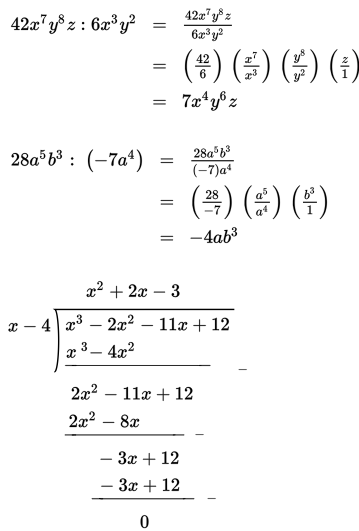
S1
Hasil dari
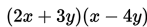
adalah ....
S2
Hasil dari
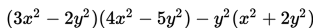
adalah ....
S3
Sebuah lahan berbentuk persegi panjang dengan panjang (2x – 3) meter dan lebar (x + 6) meter. Sekeliling lahan tersebut dibuat jalan selebar 2 meter. Luas lahan yang tersisa adalah ....
S4
Bentuk aljabar x2 + 4x - 60 jika dibagi suatu bentuk aljabar hasilnya adalah x + 10. Bentuk aljabar pembagi tersebut adalah ....
S5
Suatu bentuk aljabar memiliki tiga faktor, (x + 3), (x – 6), dan (2x + 7). Hasil pembagian bentuk aljabar tersebut jika dibagi (6 – x) adalah ....
S6
Pak Idris mempunyai kebun apel berbentuk persegi dan Pak Halim mempunyai kebun semangka berbentuk persegi panjang. Ukuran panjang kebun semangka pak Halim 10 m lebihnya dari panjang sisi kebun apel Pak Idris sedangkan lebarnya, 3 m lebih dari panjang sisi kebun apel Pak Idris. Luas kebun semangka Pak Halim adalah ... (satuan luas)
S7
Nilai e pada persamaan bentuk aljabar
(4x + 3y)(cx + dy) = ex2 + 23xy + 6y2
adalah ....
(4x + 3y)(cx + dy) = ex2 + 23xy + 6y2
adalah ....
S8
Diketahui bentuk aljabar
3x3 + 5x2 – 31x + 6 = (Ax + B)(x – 3)(x + 1) + C
berlaku untuk setiap x ∈ R.
3x3 + 5x2 – 31x + 6 = (Ax + B)(x – 3)(x + 1) + C
berlaku untuk setiap x ∈ R.
Nilai A.B.C dari bentuk tersebut adalah ....
S9
Hasil pembagian bentuk aljabar (2x3 – x2 – 5x + 2) oleh (x – 2) adalah ....
S10
Hasil pembagian bentuk aljabar (3x4 – x2 + 5x – 7) oleh (x2 + 3x – 2) adalah ....
