Contoh Soal Mengenal Fungsi Kuadrat

Contoh Soal Mengenal Fungsi Kuadrat - Apakah kalian masih ingat dengan apa yang dimaksud dengan fungsi atau pemetaan?

Materi tersebut menjadi dasar bagi kalian dalam mempelajari fungsi kuadrat.

Yuk kita ingat kembali.

Fungsi/Pemetaan

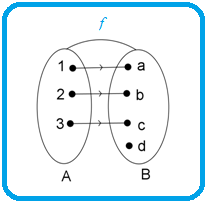
Diagram panah di atas menunjukkan suatu relasi dari himpunan $A$ ke himpunan $B$, dimana $A$ = {$1,2,3$} dan $B$ = {$a,b,c,d$}.

Jika kalian perhatikan, setiap anggota himpunan $A$ dihubungkan dengan tepat pada satu anggota himpunan $B$. Nah, relasi dengan sifat demikian disebut fungsi atau pemetaan.

Selanjutnya, karena fungsi yang memetakan himpunan $A$ ke himpunan $B$ adalah $f$, maka dapat kita tulis notasi pemetaan seperti berikut: $f:A\to B$.

Lebih lanjut, peta dari setiap $xϵA$ oleh fungsi $f$ sering dinyatakan sebagai $f(x)$ dan bentuk $f(x)$ disebut rumus fungsi $f$.

Berdasarkan diagram panah di atas, dapat kita simpulkan bahwa:

• $f$ memetakan $1$ ke $a$ → $f(1)=a$
• $f$ memetakan $2$ ke $b$ → $f(2)=b$
• $f$ memetakan $3$ ke $c$ → $f(3)=c$

Nah, sekarang kalian sudah ingat kembali mengenai fungsi/pemetaan bukan?

Yuk sekarang kita cari tahu apa itu fungsi kuadrat.

Fungsi Kuadrat

Untuk setiap $a,b,c,xϵR$, fungsi $y=f(x)=a{x}^2+bx+c$ disebut fungsi kuadrat jika a ≠ 0.

Pada fungsi $f$ di atas, $x$ adalah variabel bebas, sedangkan $y$ adalah variabel terikat.

Seperti halnya relasi, fungsi kuadrat juga mempunyai domain, kodomain, dan range.

Domain adalah daerah asal, kodomain adalah daerah kawan, dan range adalah daerah hasil.

Tahukah kalian domain, kodomain, dan range dari fungsi $f$ di atas?

Benar sekali. Domainnya adalah $xϵR$, kodomainnya adalah $yϵR$, dan rangenya adalah $f(x)$.

Bagaimana cara menentukan range fungsi?

Sebagai ilustrasi, misalkan $f(x)=x^2-2x-3$, dengan domain $–2\le x\le 4$, dimana $xϵR$.

Oleh karena $xϵR$ dan $–2\le x\le 4$, maka ada banyak kemungkinan nilai $x$. Nah, untuk mempermudah kita dalam menentukan range fungsi $f$, kita ambil nilai $x$ yang bulat.

• $f(–2)=(–2{)}^2–2(–2)–3=5$
• $f(–1)=(–1{)}^2–2(–1)–3=0$
• $f(0)=(0{)}^2–2(0)–3=–3$
• $f(1)=(1{)}^2–2(1)–3=–4$
• $f(2)=(2{)}^2–2(2)–3=–3$
• $f(3)=(3{)}^2–2(3)–3=0$
• $f(4)=(4{)}^2–2(4)–3=5$

Berdasarkan uraian di atas, tampak bahwa nilai $f(x)$ terkecil adalah $-4$, sedangkan nilai $f(x)$ terbesar adalah $5$. Dengan demikian, range fungsi $f$ adalah $–4\le y\le 5$.

Nah, setelah range fungsi diketahui, kalian dapat menggambarkan grafik fungsi kuadrat.

Bagaimanakah caranya?

Langkah pertama adalah menentukan titik yang dilalui grafik fungsi.

Berdasarkan ilustrasi di atas, titik yang dilalui oleh grafik fungsi kuadrat $f(x)=x^2-2x-3$ adalah $(–2,5)$, $(–1,0)$, $(0,–3)$, $(1,–4)$, $(2,–3)$, $(3,0)$, dan $(4,5)$.

Langkah kedua adalah menghubungkan semua titik pada koordinat Kartesius.

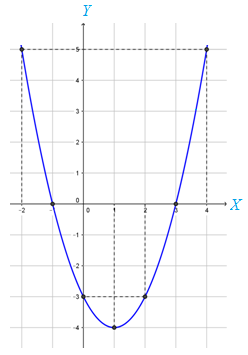
Apa yang dapat kalian simpulkan dari grafik fungsi kuadrat di atas?

Seperti yang kalian lihat,

• grafik membuka ke atas
• grafik memotong sumbu $X$ di dua titik yang berbeda, yaitu $(–1,0)$ dan $(3,0)$
• grafik memotong sumbu $Y$ di titik $(0,–3)$
• sumbu simetrinya adalah $x=1$
• titik puncaknya adalah $(1,–4)$
• nilai minimumnya adalah $–4$

Sebenarnya tanpa menggambar grafik, kalian juga dapat menebak apakah grafik tersebut terbuka ke atas, apakah grafik tersebut memotong sumbu $X$, apakah grafik tersebut memotong sumbu $Y$, koordinat titik puncak, serta nilai minimum atau maksimum fungsi.

Bagaimanakah caranya?

Yang perlu kalian lakukan adalah memperhatikan nilai $a$, $b$, dan $c$ dari fungsi kuadrat $f(x)=a{x}^2+bx+c$.

• Jika $a>0$, kurva terbuka ke atas dan memiliki nilai minimum. Jenis titik puncaknya adalah titik balik minimum.
• Jika $a<0$, kurva terbuka ke bawah dan memiliki nilai maksimum. Jenis titik puncaknya adalah titik balik maksimum.
• Persamaan sumbu simetri kurva adalah $x=-\frac{b}{2a}$ dan titik puncak kurva adalah $(-\frac{b}{2a},-\frac{D}{4a})$, dimana $D=b^2-4ac$.
• Jika nilai $a$ dan $b$ berlawanan tanda, maka titik puncak berada di sebelah kanan sumbu $Y$.
• Jika nilai $a$ dan $b$ bertanda sama, maka titik puncak berada di sebelah kiri sumbu $Y$.
• Jika $c>0$, maka kurva memotong sumbu $Y$ positif.
• Jika $c<0$, maka kurva memotong sumbu $Y$ negatif.
• Jika $D>0$, maka kurva memotong sumbu $X$ di dua titik.
• Jika $D=0$, maka kurva menyinggung sumbu $X$.
• Jika $D<0$, maka kurva tidak memotong dan tidak menyinggung sumbu $X$.

S1

Fungsi berikut yang tergolong fungsi kuadrat adalah ….

S2

Jika fungsi kuadrat $y+6=(x+3{)}^2$ dinyatakan dalam bentuk $y=a{x}^2+bx+c$, maka nilai $a+b+c$ adalah ….

S3

Pernyataan yang benar mengenai grafik fungsi kuadrat $y=-2x^2+3x+5$ adalah ….

S4

Titik potong grafik fungsi kuadrat $y=x^2+3x-10$ dengan sumbu $X$ adalah ….

S5

Titik potong grafik fungsi kuadrat $y=(x-2{)}^2-11$ dengan sumbu $Y$ adalah ….

S6

Diketahui fungsi kuadrat $y=2x^2+5x+2$. Titik potong grafik fungsi kuadrat dengan sumbu $X$ adalah $(x_1,0)$ dan $(x_2,0)$, sedangkan titik potong grafik fungsi kuadrat dengan sumbu $Y$ adalah $(0,y_1)$. Nilai dari $x_1+x_2+y_1$ adalah ….

S7

Persamaan sumbu simetri fungsi kuadrat $y=\frac{1}{2}{x}^2-4x+5$ adalah ….

S8

Titik puncak kurva parabola $y=2x^2-6x+3$ adalah …

S9

Jika kurva $y=x^2-\left(m+1\right)x+9$ menyinggung sumbu $X$, maka nilai $m$ adalah ….

S10

Nilai maksimum dari fungsi kuadrat $y=8-10x-2x^2$ adalah ….

Share this post