Contoh Soal Konsep Gradien dan Garis Lurus
Contoh Soal Konsep Gradien dan Garis Lurus - Dalam aktivitas sehari-hari, tentunya kalian pernah menggambar garis lurus, namun apakah kalian tahu bahwa setiap garis lurus mempunyai kemiringan tertentu?
Pengertian Gradien
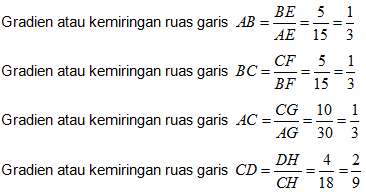
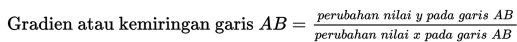
Gradien Garis pada Bidang Koordinat Cartesius

Gradien Garis yang Melalui Dua Titik
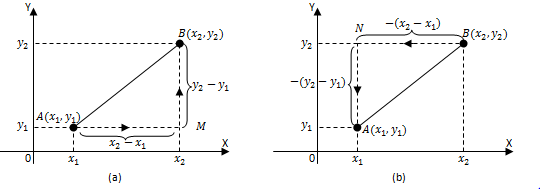
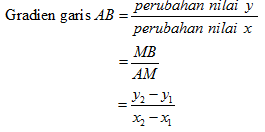
Gradien Garis yang saling Sejajar
Gradien Garis yang saling Tegak Lurus
Garis Lurus
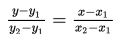
Untuk memperdalam pemahaman kalian, mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
Penyelesaian :

Contoh 2 :
Penyelesaian :
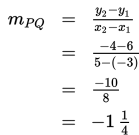
Contoh 3 :
Penyelesaian :
Contoh 4 :
Penyelesaian :
Contoh 5 :
Penyelesaian :

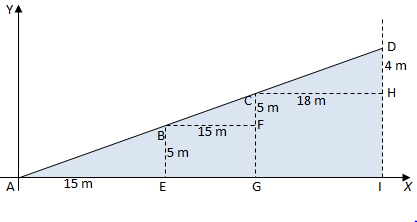
Mari kita cermati gambar ruas jalan berikut ini.

Ruas jalan dari A sampai D posisi jalannya miring. Pada ruas jalan dari A sampai B, jarak horizontalnya 15 m dan ketinggiannya 5 m, sedangkan pada ruas jalan dari C sampai D, jarak horizontalnya 18 m dan ketinggiannya 4 m.
Pengertian Gradien
Ukuran kemiringan, yang selanjutnya disebut gradien, untuk masing-masing ruas garis pada gambar di atas dapat ditentukan dengan cara berikut.
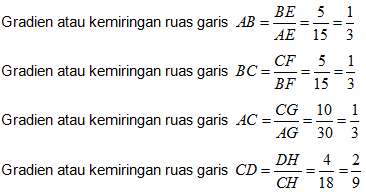
- AE, BF, AG, dan CH merupakan perubahan jarak mendatar yang selanjutnya disebut dengan perubahan nilai x atau perubahan jarak mendatar.
- BE, CF, CG, dan DH merupakan perubahan jarak tegak yang selanjutnya disebut dengan perubahan nilai y atau perubahan jarak tegak.
Dengan kata lain, gradien merupakan nilai perbandingan antara perubahan nilai y dengan perubahan nilai x.
Perhatikan gradien ruas garis AB, BC, dan AC pada uraian di atas. Ternyata ketiga ruas garis tersebut memiliki gradien yang sama, yaitu 1/3 , walaupun panjangnya berbeda.
Jadi, gradien garis tidak tergantung pada panjang garis.
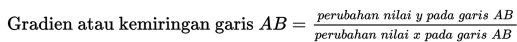
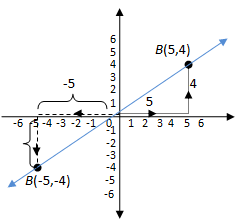
Gradien Garis pada Bidang Koordinat Cartesius
Perhatikan gambar di bawah ini.

Pada garis k , terdapat ruas garis OA dan OB dengan koordinat O(0 , 0), A(5 , 4), dan B(-5 , -4).
Dengan demikian,

Jadi, gadien garis k = gradien OA = gradien OB = 4/5
Berdasarkan uraian di atas, dapat ditarik kesimpulan sebagai berikut :
- Untuk menentukan gradien garis k, kita perlu memilih salah satu ruas garis pada garis k, misal : garis OA atau OB.
- Perubahan nilai x bernilai positif jika bergerak ke kanan (dari O bergerak ke C)
- Perubahan nilai x bernilai negatif jika bergerak ke kiri (dari O bergerak ke D)
- Perubahan nilai y bernilai positif jika bergerak ke atas (dari C bergerak ke A)
- Perubahan nilai y bernilai negatif jika bergerak ke bawah (dari D bergerak ke B)
- Garis dengan kemiringan seperti garis k mempunyai gradien bernilai positif
Gradien Garis yang Melalui Dua Titik
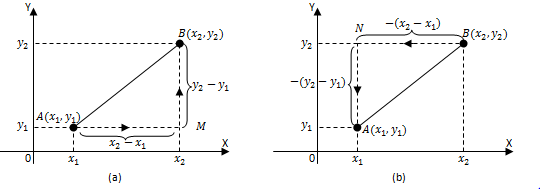
Perhatikan titik A(x1 , y1) dan B(x2 , y2) pada gambar di atas.
Untuk menentukan gradien garis AB pada gambar (a), terlebih dahulu kita tentukan perubahan nilai x dan perubahan nilai y dari garis AB.
- Perubahan nilai x garis AB = AM = x2 - x1
- Perubahan nilai y garis AB = MB = y2 - y1
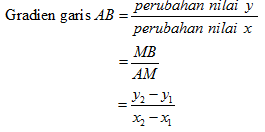
Untuk selanjutnya, gradien garis AB dapat ditulis mAB
Gradien Garis yang saling Sejajar
Garis-garis yang sejajar memiliki gradien yang sama.
m1 = m2
m1 = m2
Gradien Garis yang saling Tegak Lurus
Hasil kali gradien antara kedua garis yang saling tegak lurus adalah (-1)
m1 X m2 = - 1
m1 X m2 = - 1
Garis Lurus
Bentuk umum dari persamaan garis lurus adalah y = mx + c atau ax + by = c
Selanjutnya,
1. gradien dari garis y = mx + c adalah m
2. gradien dari garis ax + by = c adalah -a/b
1. gradien dari garis y = mx + c adalah m
2. gradien dari garis ax + by = c adalah -a/b
Aksioma : melalui dua buah titik hanya dapat dibuat sebuah garis lurus.
Dengan demikian, hanya ada satu garis yang melalui titik (x1 , y1) dan (x2 , y2) , yaitu :
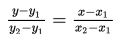
Untuk memperdalam pemahaman kalian, mari kita mencermati beberapa contoh soal berikut ini.
Contoh 1 :
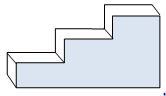
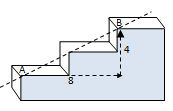
Gambar di bawah menunjukkan tampak samping dari bagian tangga beton. Hitunglah gradien tangga tersebut!

Penyelesaian :
Untuk menentukan gradien, kita perlu membuat garis yang melalui pojok-pojok atas tangga seperti gambar di bawah.


Contoh 2 :
Tentukan gradien garis yang menghubungkan pasangan titik P(- 3, 6) dan Q(5, - 4).
Penyelesaian :
- Karena P(-3 , 6) maka x1 = -3 dan y1 = 6
- Karena P(5 , -4) maka x1 = 5 dan y1 = -4
Dengan demikian,
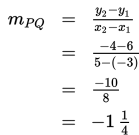
Contoh 3 :
Garis g yang bergradien -5/3 sejajar dengan garis l. Tentukan gradien garis l !
Penyelesaian :
Karena garis l sejajar dengan garis g, maka ml = mg = -5/3
Contoh 4 :
Garis k yang bergradien 2/5 tegak lurus dengan garis l. Tentukan gradien garis l !
Penyelesaian :
Karena garis l sejajar dengan garis k, maka ml X mk = -1 <=> ml = -1/mk = -5/2
Contoh 5 :
Tentukan gradien dari garis berikut :
1. 6x + 4y = 12
2. 3x - 8y + 15 =0
1. 6x + 4y = 12
2. 3x - 8y + 15 =0
Penyelesaian :
1. 6x + 4y = 12 => m = -a/b = -6/4 = -3/2
2. 3x - 8y + 15 = 0 => m = -a/b = -3/(-8) = 3/8
2. 3x - 8y + 15 = 0 => m = -a/b = -3/(-8) = 3/8
S1
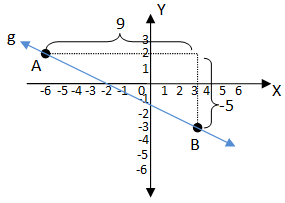
Perhatikan gambar berikut ini.

Gradien garis g adalah ....
S2
Diketahui titik A(-7 , 2n) dan B(-3n , 6). Nilai n jika gradien garis AB = 2 adalah ....
S3
Perhatikan tabel berikut.

Titik A, B, dan C terletak pada satu garis lurus (kolinear). Nilai n adalah ....
S4
Gradien garis yang melalui titik (9, - 7) dan (3, 8) adalah ....
S5
Jika gradien garis yang melalui titik R(-1 , a) dan S(-4 , -2a) adalah 2, maka nilai a adalah ....
S6
Garis dengan persamaan ax + by = 8 melalui titik (3 , -2) dan (2 , 4). Nilai a dan b berturut-turut adalah ....
S7
Gradien garis yang melalui titik (-5 , 2p) dan (-1 , p) memiliki kemiringan yang sama dengan garis yang melalui titik (1 , 2) dan (3 , 1). Nilai p adalah ....
S8
Garis yang melalui titik A(-2 , 3) dan B(2 , p) memiliki kemiringan ½ . Nilai p adalah ....
S9
Kemiringan garis yang melalui titik P(4 , h) dan Q(h + 3 , 7) adalah -1/4 . Nilai h adalah ....
S10
Garis l1 melalui titik (2 , -3) dan (4 ,1) dan garis l2 melalui titik (5 , -6) dan (-3 , -2). Hubungan antara kedua garis tersebut adalah ....
