Contoh Soal Persamaan Garis Lurus Jika Diketahui Gradien
Contoh Soal Persamaan Garis Lurus Jika Diketahui Gradien - Pernahkah kalian memperhatikan kemiringan atap genteng rumah kita? Seandainya atap rumah kita buat terlalu miring akan menyulitkan pada saat pemasangan maupun saat penggantian genting karena atap tersebut sulit dipanjat. Sedangkan apabila kurang miring akan menyebabkan air hujan tidak cepat turun. Kemiringan tersebut selanjutnya kita kenal dengan nama gradien.
Gradien adalah nilai yang menyatakan kecondongan (kemiringan) suatu garis.
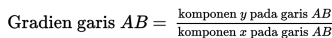
Gradien Garis
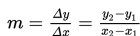
Nah, kita sekarang akan belajar menentukan persamaan garis jika gradiennya diketahui.
Persamaan garis melalui titik (x1,y1) dengan gradien m
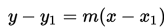
Agar kalian lebih paham, mari kita perhatikan beberapa contoh soal berikut ini.
Contoh 1 :
Contoh 2 :
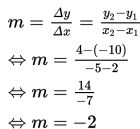
Sekarang, mari kita akan mempelajari tentang garis lurus. Untuk itu, marilah kita mengingat terlebih dahulu yang berkaitan dengan gradien garis.
Gradien adalah nilai yang menyatakan kecondongan (kemiringan) suatu garis.
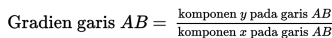
Gradien garis bernilai
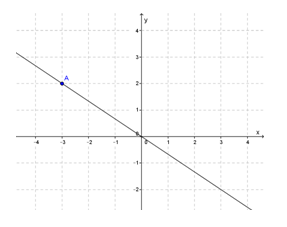
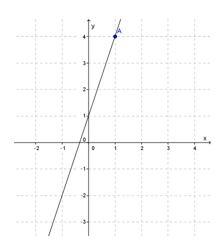
1. positif jika garis condong ke kanan
2. negatif jika garis condong ke kiri
1. positif jika garis condong ke kanan
2. negatif jika garis condong ke kiri
Gradien Garis
Gradien garis melalui dua titik : A(x1 , y1) dan B(x2 , y2) adalah :
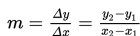
Nah, kita sekarang akan belajar menentukan persamaan garis jika gradiennya diketahui.
Persamaan garis melalui titik (x1,y1) dengan gradien m
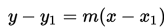
Agar kalian lebih paham, mari kita perhatikan beberapa contoh soal berikut ini.
Contoh 1 :
Tentukan persamaan garis yang melalui titik (4,3) dan bergradien – 2.
Penyelesaian :
Persamaan garis melalui titik (x1 , y1) dengan gradien m adalah :
y - y1 = m(x - x1)
y - y1 = m(x - x1)
Dengan demikian, persamaan garis yang melalui titik (4,3) dan bergradien –2 adalah
y – 3 = –2(x – 4)
<=> y = –2x + 8 + 3
<=> y = –2x + 11
y – 3 = –2(x – 4)
<=> y = –2x + 8 + 3
<=> y = –2x + 11
Contoh 2 :
Diketahui m adalah gradien garis yang melalui titik P(2,–10) dan Q(–5,4). Tentukan persamaan garis yang melalui titik (–6,2) dan bergradien m.
Penyelesaian :
Gradien garis yang melalui titik P(2,–10) dan Q(–5,4) adalah :
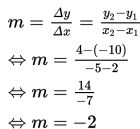
Dengan demikian, persamaan garis yang melalui titik (– 6,2) dan bergradien m= –2 adalah :
y – 2 = –2(x + 6)
<=> y = –2x – 12 + 2
<=> y = –2x – 12 + 2
S1
Persamaan garis melalui titik (2,1) dengan gradien 4 adalah ....
S2
Garis yang melalui titik ( – 1 , 3) dengan gradien 2/3 adalah ....
S3
Persamaan garis melalui pusat koordinat kartesius dan bergradien - ¾ adalah ....
S4
Diketahui m adalah gradien garis yang melalui titik A(-4,7) dan B(2,-2). Persamaan garis melalui titik (3, 5) dengan gradien m adalah ....
S5
Garis y = -2x + 8 merupakan garis yang melalui ....
S6
Persamaan garis melalui titik (0,3) dan bergradien 6 adalah ....
S7
Garis melalui titik (5,1) dan bergradien – 3 memotong sumbu y pada titik ....
S8
Persamaan garis g pada gambar berikut ini adalah ....

S9
Persamaan garis g dalam gambar berikut ini adalah ....

S10
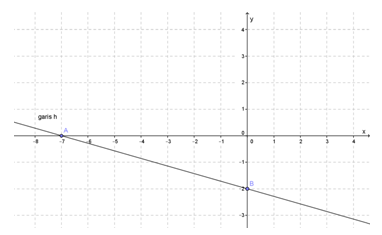
Perhatikan gambar garis h berikut ini.

Garis h tersebut mempunyai gradien m. Persamaan garis melalui titik (-4,3) dengan gradien m adalah ....
