Contoh Soal Penggunaan Turunan dalam Kehidupan Sehari-hari

Contoh Soal Penggunaan Turunan dalam Kehidupan Sehari-hari - Topik ini merupakan topik terakhir dari materi turunan. Pada topik ini, kalian akan belajar bagaimana memodelkan dan menyelesaikan masalah dalam kehidupan sehari-hari yang melibatkan turunan. Salah satu konsep turunan yang sering digunakan adalah turunan pertama dan nilai maksimum serta minimum fungsi. Konsep turunan pertama fungsi banyak digunakan dalam masalah kecepatan dengan diketahui fungsi posisinya, sedangkan konsep nilai maksimum dan minimum fungsi digunakan dalam masalah luas seperti luas tanah dan bangunan, volume bangun ruang, dan ilmu ekonomi.

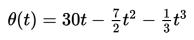
        Nilai maksimum dan minimum suatu fungsi sering disebut dengan nilai ekstrim. Nilai ekstrim dari fungsi y=f(x)$y=f\left(x\right)$ diperoleh untuk x$x$ yang memenuhi persamaan f′(x)=0$f^{\prime }\left(x\right)=0$. Jika x=a$x=a$ adalah nilai x$x$ yang memenuhi persamaan f′(x)=0$f^{\prime }\left(x\right)=0$, maka (a,f(a))$\left(a,f\left(a\right)\right)$ adalah titik ekstrim fungsi y=f(x)$y=f\left(x\right)$ dan f(a)$f\left(a\right)$ adalah nilai ekstrim fungsi y=f(x)$y=f\left(x\right)$. 
Jenis nilai ekstrim fungsi dapat ditentukan sebagai berikut.

• Nilai ekstrim ini akan merupakan nilai maksimum jika:

f ' (x) = 0 dan f “ (x) < 0.

• Nilai ekstrim akan merupakan nilai minimum jika:

f '(x) = 0 dan f “ (x) > 0.

SOAL 1

Suatu proyek pembangunan gedung sekolah dapat diselesaikan dalam x hari dengan biaya proyek per hari

(5x−1000+200x)$$\left(5\mathit{x}-1000+\frac{200}{\mathit{x}}\right)$$

ratus ribu rupiah. Agar biaya proyek minimum maka proyek tersebut harus diselesaikan dalam waktu .…

SOAL 2

Rusuk suatu kubus bertambah panjang dengan kelajuan 7 cm per detik. Laju bertambahnya volume pada saat panjang rusuk 15 cm adalah ….

SOAL 3

Sebuah roda mobil berputar pada sumbunya. Pada waktu t$t$, jari-jari roda mobil sudah berputar dengan sudut:
R (t) = 128t - 2t2 . 
Kelajuan perubahan kecepatan sudutnya adalah ….

SOAL 4

Jarak yang ditempuh sebuah bus pariwisata dalam waktu t diberikan oleh fungsi s (t) = −23$-\frac{2}{3}$ t3+ 4t2 - t. Kecepatan maksimum bus pariwisata itu dicapai pada saat t = ....

SOAL 5

Sebuah kapur barus berbentuk tabung memiliki diameter alas sama dengan tingginya. Kapur barus tersebut menyublim sedemikian rupa sehingga selalu berbentuk tabung yang diameter alasnya sama dengan tinggi tabung. Laju perubahan volume kapur barus terhadap tinggi pada saat tingginya 4 satuan adalah ....

SOAL 6

Sebuah roda berputar mengelilingi titik pusatnya. Sudut simpangan setiap titik pada roda tersebut pada waktu t$t$ dirumuskan sebagai berikut :

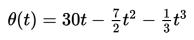
Besar sudut θ pada waktu kecepatan sudutnya sama dengan nol adalah .…

SOAL 7

Suatu perusahaan menghasilkan x produk dengan biaya total sebesar (25 + 5x + x2) rupiah. Jika semua produk perusahaan tersebut terjual dengan harga Rp65,00 untuk setiap produknya, maka laba maksimum yang dapat diperoleh perusahaan adalah ….

SOAL 8

Dua buah kandang letaknya saling berdampingan, masing-masing mempunyai ukuran x$x$ m x v$v$ m dengan luas setiap kandang adalah 36 m2. Agar panjang pagar yang digunakan untuk memagari kandang jumlahnya sekecil mungkin, maka panjang x$x$ dan v$v$berturut-turut adalah ….

SOAL 9

Sebuah triplek berbentuk persegi dengan panjang sisi a$a$ cm akan dibuat menjadi sebuah kotak mainan tanpa tutup dengan cara memotong empat persegi di bagian pojok triplek dengan panjang sisi x$x$ cm. Volume kotak akan maksimum untuk nilai x$x$ sama dengan ….

SOAL 10

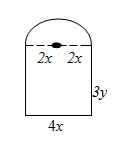
Sebuah pintu mempunyai bentuk seperti pada gambar di bawah ini.

Jika keliling pintu sama dengan p$p$, maka luas pintu akan maksimum untuk x$x$ = ….

Share this post