Contoh Soal Pengantar kepada Persamaan Gerak
Contoh Soal Pengantar kepada Persamaan Gerak - Pikirkan sebuah obyek yang bergerak dengan sebuah
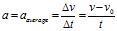
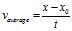
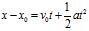
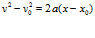
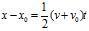
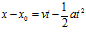
percepatan yang konstan di sepanjang sebuah garis (misal, sebuah mobil yang sedang menambah kecepatan). Dalam hal
ini, percepatan tidak bergantung pada waktu karena:
ini, percepatan tidak bergantung pada waktu karena:
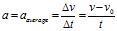
atau
v = v0 + at (1),
dimana v0 adalah velositas mula-mula pada
waktu t = 0 det. Di sisi lain, bila percepatannya adalah negatif kita memiliki:
dimana v0 adalah velositas mula-mula pada
waktu t = 0 det. Di sisi lain, bila percepatannya adalah negatif kita memiliki:
v = v0 - at (2).
Persamaan-persamaan (1) dan (2)persamaan-persamaan tingkat pertama yang di dalamnya waktu adalah variabel utamanya dan hanya digunakan dengan pangkat satu. Oleh karena itu, persamaan-persamaan ini
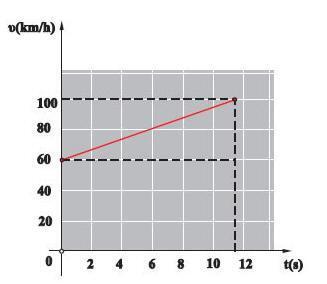
diwakili oleh sebuah garis lurus dalam grafik velositas-waktu, sebagaimana digambarkan dalam contoh dalam Gambar 1 (di bawah).
Persamaan-persamaan (1) dan (2)persamaan-persamaan tingkat pertama yang di dalamnya waktu adalah variabel utamanya dan hanya digunakan dengan pangkat satu. Oleh karena itu, persamaan-persamaan ini
diwakili oleh sebuah garis lurus dalam grafik velositas-waktu, sebagaimana digambarkan dalam contoh dalam Gambar 1 (di bawah).

Lereng dari grafik tersebut, sebagaimana telah kita pelajari dari (1) dan (2),
menyajikan nilai percepatannya. Lebih lagi, dari pelajaran-pelajaran sebelumnya kita mengetahui bahwa velositas rata-ratanya adalah sama dengan:
menyajikan nilai percepatannya. Lebih lagi, dari pelajaran-pelajaran sebelumnya kita mengetahui bahwa velositas rata-ratanya adalah sama dengan:
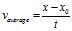
dimana x dan x0 adalah nilai-nilai perpindahan pada waktu t dan waktu nol, secara berturut-turut.
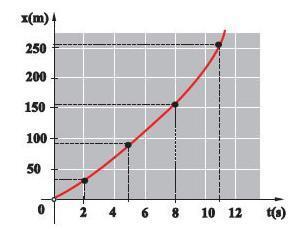
Jika obyek tersebut memiliki sebuah nilai percepatan yang konstan dan memiliki suatu perpindahan awal sebesar x0 dan sebuah velositas mula-mula v0, maka kita dapat menemukan jarak yang telah dilaluinya dalam waktu t dengan menggunakan persamaan:
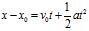
(3). Persamaan (3) adalah tingkat kedua
dalam hal waktunya, dan oleh karena itu grafik perpindahan-waktunya yang cocok adalah sebuah kurva. Salah satu kemungkinan contoh digambarkan dalam Gambar 2 (di bawah ini).
dalam hal waktunya, dan oleh karena itu grafik perpindahan-waktunya yang cocok adalah sebuah kurva. Salah satu kemungkinan contoh digambarkan dalam Gambar 2 (di bawah ini).

Persamaan-persamaan (1) dan (3)
membentuk dasar bagi perhitungan-perhitungan mengenai gerakan dari sebuah obyek dalam suatu garis lurus, dengan mengasumsikan bahwa percepatan dari obyek tersebut adalah konstan. Persamaan-persamaan lain yang secara aljabar diturunkan dari persamaan-persamaan ini terbukti amat sangat
membantu dalam perhitungan-perhitungan kita jika beberapa kuantitas tidak diketahui atau memang tidak tersedia. Sebagai contoh, persamaan:
membentuk dasar bagi perhitungan-perhitungan mengenai gerakan dari sebuah obyek dalam suatu garis lurus, dengan mengasumsikan bahwa percepatan dari obyek tersebut adalah konstan. Persamaan-persamaan lain yang secara aljabar diturunkan dari persamaan-persamaan ini terbukti amat sangat
membantu dalam perhitungan-perhitungan kita jika beberapa kuantitas tidak diketahui atau memang tidak tersedia. Sebagai contoh, persamaan:
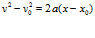
(4) menjelaskan hubungan antara velositas, percepatan, dan perpindahan. Persamaan (4) tergantung
pada waktu dan oleh karenanya dapat menjadi sangat berguna dalam soal-soal dimana kita ingin menemukan, misalnya, velositas mula-mula dari sebuah obyek tanpa mengetahui waktu perjalanannya.
Persamaan sejenis yang lainnya adalah:
pada waktu dan oleh karenanya dapat menjadi sangat berguna dalam soal-soal dimana kita ingin menemukan, misalnya, velositas mula-mula dari sebuah obyek tanpa mengetahui waktu perjalanannya.
Persamaan sejenis yang lainnya adalah:
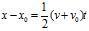
(5). Untuk
sebuah soal dimana nilai percepatannya tidak diketahui, (5) sangatlah membantu
untuk menentukan, misalnya, waktu atau posisi awal dari sebuah obyek yang bergerak.
Akhirnya,
bila kita menginginkan sebuah persamaan yang menjelaskan sebuah benda bergerak yang mengesampingkan kecepatan awalnya, kita dapat menggunakan yang berikut:
sebuah soal dimana nilai percepatannya tidak diketahui, (5) sangatlah membantu
untuk menentukan, misalnya, waktu atau posisi awal dari sebuah obyek yang bergerak.
Akhirnya,
bila kita menginginkan sebuah persamaan yang menjelaskan sebuah benda bergerak yang mengesampingkan kecepatan awalnya, kita dapat menggunakan yang berikut:
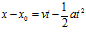
(6). Persamaan ini berguna untuk menghitung, sebagai contoh, perpindahan atau velositas pada suatu waktu tertentu dengan mengetahui nilai perpindahan awalnya.
Seara umum, untuk latihan apapun yang melibatkan pergerakan dalam sebuah garis lurus yang di dalamnya nilai percepatannya diketahui bersifat konstan, kita harus selalu menuliskan kuantitas yang tersedia dan kuantitas-kuantitas yang sedang kita cari. Kita dapat selalu kembali pada persamaan-persamaan (1) sampai (6), menentukan mana yang paling berguna berdasar apa yang kita ketahui, dan menghitung hasilnya yang benar dengan menggunakan persamaan yang terbaik. Marilah kita mencoba sebuah contoh. Seandainya sebuah mobil
bergerak dengan velositas awal 72 km/jam, dan kita ingin menghitung perpindahan dan waktu yang diperlukan bagi mobil tersebut untuk berhenti sejak saat mobil tersebut mulai mengerem dengan tingkat perlambatan 10 m/det2. Kuantitas-kuantitas yang telah kita ketahui adalah
velositas awalnya (v0), velositas akhirnya yaitu nol (v), dan perlambatannya (a); kita ingin mengetahui posisi (x) dan waktu (t) akhir yang dicapainya. Pertama, kita tahu bahwa 72 km/jam adalah sama dengan 20 m/det.
bergerak dengan velositas awal 72 km/jam, dan kita ingin menghitung perpindahan dan waktu yang diperlukan bagi mobil tersebut untuk berhenti sejak saat mobil tersebut mulai mengerem dengan tingkat perlambatan 10 m/det2. Kuantitas-kuantitas yang telah kita ketahui adalah
velositas awalnya (v0), velositas akhirnya yaitu nol (v), dan perlambatannya (a); kita ingin mengetahui posisi (x) dan waktu (t) akhir yang dicapainya. Pertama, kita tahu bahwa 72 km/jam adalah sama dengan 20 m/det.
Menggunakan (2), kita mempunyai:
v = v0 - at, yang dengan pengurangan ini menghasilkan:
0 = 20 - 10 x t, yang dapat secara aljabar dimanipulasikan untuk menghasilkan t = 2 det. sebagai waktu dicapainya posisi akhir tersebut.
Sekarang, menggunakan (3), kita mempunyai:
x - x0 = v0t + (1/2)at2, yang dengan substitusi menghasilkan:
x - x0 = 20(2) + (1/2)(-10)(22), yang dapat dihitung untuk menghasilkan sebuah perpindahan sebesar 40 - 20 = 20 m, dengan asumsi x0 adalah nol.
S1
Sebuah benda bergerak dengan percepatan 10 m/s2 ( a = 10 m/s2) selama 4 s. Jika kecepatan akhir benda tersebut 52 m/s, maka kecepatan awalnya adalah....
S2
Sebuah peluru ditembakkan dari sebuah senjata dan bertambah cepat dalam suatu jarak x = 0.34 m, di dalam laras senjata tersebut, sebelum keluar setelah 9.5 mdet. Berapa percepatan peluru tersebut di dalam laras senjata tersebut?
S3
Velositas dari seorang pria yang naik sepeda motor adalah 7 m / det. Dia mulai mempercepat diri dan mencapai kecepatan 22,6 m / det dalam jarak 57,72 m. Berapakah percepatan sepeda motor tersebut?
S4
Seekor elang yang perkasa terbang tinggi saat mencari mangsa. Melihat seekor kelinci tepat di bawah, elang tersebut menukik dengan velositas awal 30 m/det dan mempercepatnya dengan a = 40 m/det2 hingga mencapai velositas 100 m/det, nyaris kehilangan kelinci itu dari cakarnya. Berapa ketinggian awal elang tersebut?
S5

Sebuah mobil dengan suatu velositas awal 37 km/jam berjalan naik di sebuah jalan curam. Setelah mencapai puncak bukit, mobil tersebut mulai berjalan turun dengan kecepatan konstan 66 km/jam. Berapakah kecepatan rata-rata mobil tersebut untuk keseluruhan perjalanan tersebut? Asumsikan bahwa jarak tempuh naik dan turun bukit tersebut adalah sama.
S6
Sebuah mobil yang melaju secepat 30 m/det. berada 10 m dari sebuah lampu lalu lintas. Sopirnya tiba-tiba sadar bahwa lampunya telah berubah menjadi merah, maka, ia mulai melambat pada tingkat a = -50 m/det2. Apakah sopir tersebut berhasil berhenti sebelum mencapai persimpangan? Seberapa jauhkah mobil tersebut masih melaju sebelum pada akhirnya berhenti sama sekali?
S7
Dua mobil bergerak dengan velositas yang sama, v = 80 km/jam, dan mobil yang kedua adalah x = 30 m di belakang yang pertama. Sopir dalam mobil yang kedua memutuskan untuk melewati mobil yang pertama, dan oleh karena itu mempercepatnya dengan a = 0,975 m/det2. Berapakah waktu yang dibutuhkan sopir mobil yang kedua untuk melewati mobil yang pertama, dengan asumsi bahwa ia harus setidaknya sepanjang mobilnya sendiri ditambah x2 = 2 m di depan mobil yang pertama untuk melewati? Asumsikan bahwa panjang dari kedua mobil tersebut adalah x3 = 4 m.
S8
Dua mobil bergerak dengan velositas yang sama, v = 80 km/jam, dan mobil yang kedua berada x = 30 m di belakang yang pertama. Sopir dalam mobil yang kedua memutuskan untuk melewati mobil yang pertama, dan karena itu mempercepatnya dengan a = 0,975 m/det2. Berapakah kecepatan dari mobil kedua tepat setelah melalui mobil yang pertama? Dapatlah diterima untuk menggunakan t yang dibulatkan ke detik terdekat.
S9
Seekor singa lapar sedang beristirahat. Tiba-tiba, ia melihat seekor kelinci 30 m jauhnya dan mulai mempercepat langkah untuk menangkapnya. Setelah 3.16 detik ia mencegat si kelinci dengan tiba-tiba dan menangkapnya! Berapa percepatan si singa tersebut, dengan asumsi bahwa kelinci tersebut tidak pernah berpindah untuk melarikan diri?
S10
Sebuah mobil cepat berjalan dengan suatu kecepatan yang konstan. Si sopir melihat lampu merah 300m di depan, dan karena itu ia mulai melambat pada tingkat a = 6 m/det2. Dia sangat beruntung, karena mobil tersebut berhenti persis di tempat lampu lalu lintas tersebut berada! Berapa lama waktu yang dibutuhkan mobil tersebut untuk berhenti?
