Contoh Soal Menggambar Kurva Hiperbola
Contoh Soal Menggambar Kurva Hiperbola - Dalam topik ini kalian akan belajar tentang menggambar kurva hiperbola. Topik ini sangat berkaitan dengan topik konsep hiperbola. Oke, mari kita mulai topik ini. Tetap fokus!!!
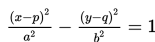
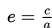
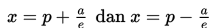
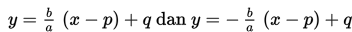
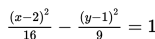
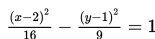
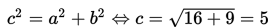
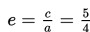
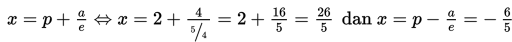
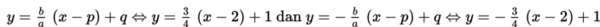
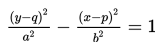
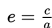
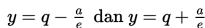
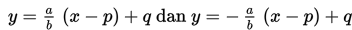
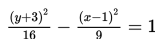

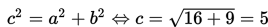
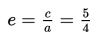
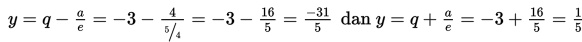
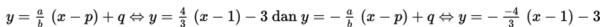
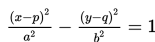
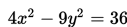

- Menggambar Kurva Hiperbola
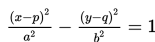
Hiperbola ini berpusat di M(p,q), sumbu utama sejajar dengan sumbu X, panjang sumbu mayor 2a, dan panjang sumbu minor 2b.
Langkah-langkah dalam menggambar kurva parabola adalah :
a. Menentukan koordinat titik pusat M(p,q).
b. Menentukan persamaan sumbu utama (y = q) dan persamaan sumbu imajiner (x = p).
c. Menentukan koordinat titik puncak yaitu A(p+a,q) dan A’(p-a,q),
d. Menentukan koordinat titik ujung sumbu minor yaitu B(p,q-b) B dan B’(p,q+b).
e. Menentukan koordinat titik fokus yaitu F1(p-c,q) dan F2(p+c,q).
f. Menentukan nilai eksentrisistas
Langkah-langkah dalam menggambar kurva parabola adalah :
a. Menentukan koordinat titik pusat M(p,q).
b. Menentukan persamaan sumbu utama (y = q) dan persamaan sumbu imajiner (x = p).
c. Menentukan koordinat titik puncak yaitu A(p+a,q) dan A’(p-a,q),
d. Menentukan koordinat titik ujung sumbu minor yaitu B(p,q-b) B dan B’(p,q+b).
e. Menentukan koordinat titik fokus yaitu F1(p-c,q) dan F2(p+c,q).
f. Menentukan nilai eksentrisistas
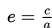
g. Menentukan persamaan direktriks yaitu
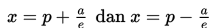
h. Menentukan persamaan asimtot yaitu
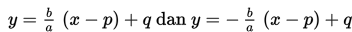
Contoh 1
Gambarlah kurva hiperbola
Gambarlah kurva hiperbola
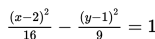
Penyelesaian:
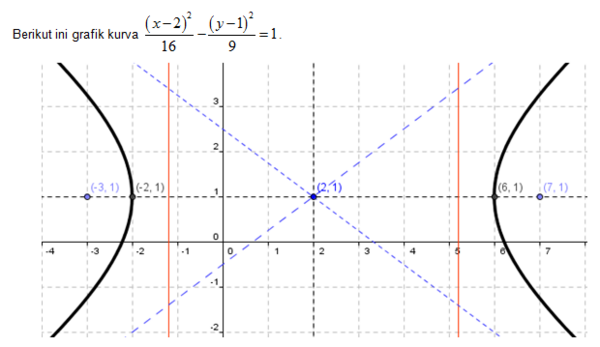
Dari persamaan hiperbola
Dari persamaan hiperbola
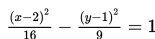
diperoleh nilai p = 2, q = 1, a2 = 16 <=> a = 4, b2 = 9 <=> b = 3. Selanjutnya, kita cari nilai c dengan
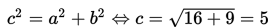
a. Koordinat titik pusat adalah M(p,q) = M(2,1).
b. Persamaan sumbu utama adalah y = 1, persamaan sumbu imajiner adalah x = 2.
c. Koordinat titik puncaknya adalah A(p+a,q) = A(6,1)dan A’(p-a,q) = A’(-2,1).
d. Koordinat titik ujung sumbu minor adalah B(p,q-b) = B(2,-2) dan B’(p,q+b) = B(2,4)
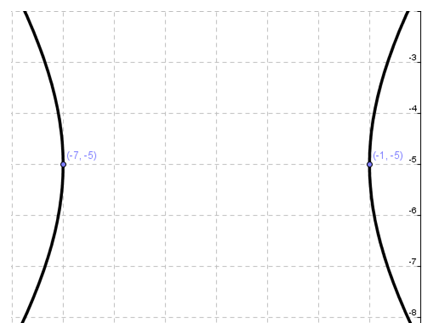
e. Koordinat titik fokus di F1(p-c,q) = F1(-3,1) dan F2(p+c,q) = F2(7,1).
f. Nilai eksentrisistas
b. Persamaan sumbu utama adalah y = 1, persamaan sumbu imajiner adalah x = 2.
c. Koordinat titik puncaknya adalah A(p+a,q) = A(6,1)dan A’(p-a,q) = A’(-2,1).
d. Koordinat titik ujung sumbu minor adalah B(p,q-b) = B(2,-2) dan B’(p,q+b) = B(2,4)
e. Koordinat titik fokus di F1(p-c,q) = F1(-3,1) dan F2(p+c,q) = F2(7,1).
f. Nilai eksentrisistas
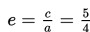
g. Persamaan direktriks adalah
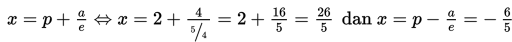
h. Persamaan asimtot adalah
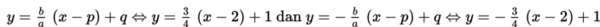

- Menggambar Kurva Hiperbola
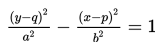
Hiperbola ini berpusat di M(p,q), sumbu utama sejajar dengan sumbu Y, panjang sumbu mayor 2a, dan panjang sumbu minor 2b.
Langkah-langkah dalam menggambar kurva hiperbola :
a. Menentukan koordinat titik pusat M(p,q).
b. Menentukan sumbu utama (x = p) dan sumbu imajiner (y = q).
c. Menentukan Koordinat titik puncak yaitu A(p,q+a) dan A’(p,q-a)
d. Menentukan koordinat titik ujung sumbu minor yaitu B(p-b,q) dan B’(p+b,q).
e. Menentukan koordinat titik fokus yaitu F1(p,q-c) dan F2(p,q+c)
f. Menentukan nilai eksentrisistas
Langkah-langkah dalam menggambar kurva hiperbola :
a. Menentukan koordinat titik pusat M(p,q).
b. Menentukan sumbu utama (x = p) dan sumbu imajiner (y = q).
c. Menentukan Koordinat titik puncak yaitu A(p,q+a) dan A’(p,q-a)
d. Menentukan koordinat titik ujung sumbu minor yaitu B(p-b,q) dan B’(p+b,q).
e. Menentukan koordinat titik fokus yaitu F1(p,q-c) dan F2(p,q+c)
f. Menentukan nilai eksentrisistas
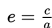
g. Menentukan persamaan direktris yaitu
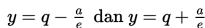
h. Menentukan persamaan asimtot yaitu
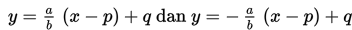
Contoh 2
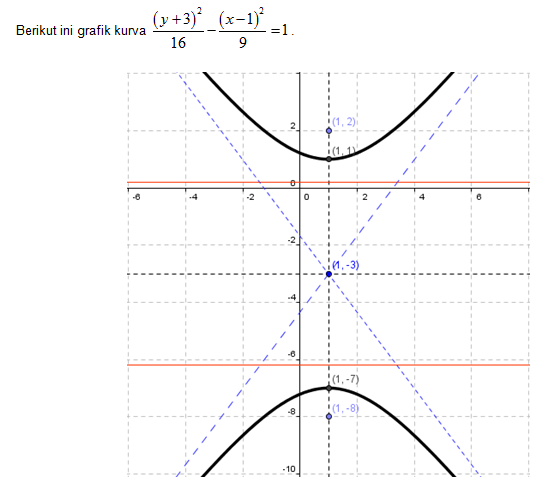
Gambarlah kurva hiperbola
Gambarlah kurva hiperbola
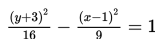
Penyelesaian:
Dari persamaan hiperbola
Dari persamaan hiperbola

diperoleh nilai p = 1, q = -3, a2 = 16 <=> a = 4, b2 = 9 <=> b = 3.
Kita cari nilai c dengan
Kita cari nilai c dengan
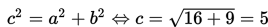
a. Koordinat titik pusat M(p,q) = M(1,-3).
b. Persamaan sumbu utama adalah x = 1, persamaan sumbu imajiner adalah y = -3.
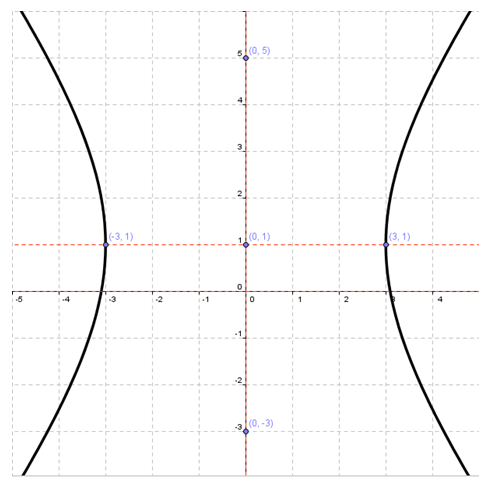
c. Koordinat titik puncak adalah A(p,q+a) = A(1,1) dan A’(p,q-a) = A(1,-7).
d. Koordinat titik ujung sumbu minor adalah B(p-b,q) = B(-2,-3) dan B’(p+b,q) = B(4,-3).
e. Koordinat titik fokus di F1(p,q-c) = F1(1,-8) dan F2(p,q+c) = F2(1,2)
f. Nilai eksentrisistas
b. Persamaan sumbu utama adalah x = 1, persamaan sumbu imajiner adalah y = -3.
c. Koordinat titik puncak adalah A(p,q+a) = A(1,1) dan A’(p,q-a) = A(1,-7).
d. Koordinat titik ujung sumbu minor adalah B(p-b,q) = B(-2,-3) dan B’(p+b,q) = B(4,-3).
e. Koordinat titik fokus di F1(p,q-c) = F1(1,-8) dan F2(p,q+c) = F2(1,2)
f. Nilai eksentrisistas
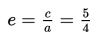
g. Persamaan direktris adalah
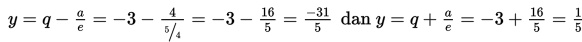
h. Persamaan asimtot adalah
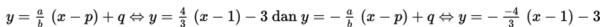

S1
Grafik kurva hiperbola
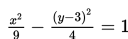
adalah....
S2
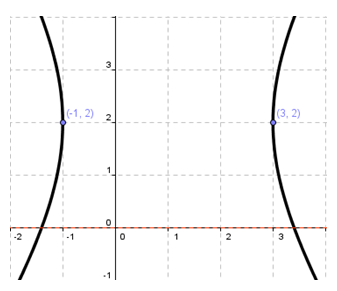
Persamaan kurva hiperbola di bawah ini adalah ….

S3
Salah satu koordinat titik fokus kurva parabola di bawah ini adalah ….

S4
Diketahui persamaan hiperbola
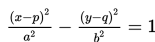
, dengan a2 + b2 = 36. Nilai eksentrisitas dari kurva parabola berikut adalah...

S5
Grafik kurva hiperbola
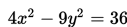
adalah....
S6
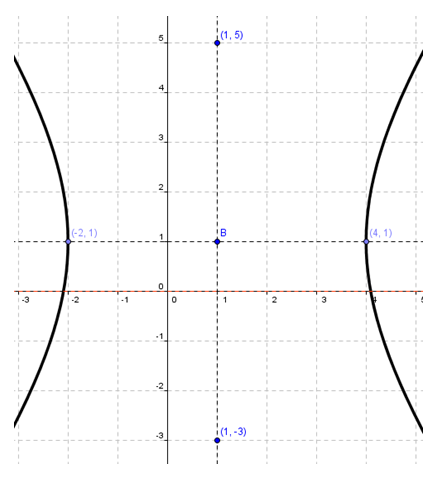
Perhatikan gambar berikut ini.

Persamaan kurva hiperbola tersebut adalah ….
S7
Salah satu persamaan asimtot untuk parabola berikut adalah...

S8
Koordinat titik pusat kurva parabola berikut adalah...

S9
Salah satu persamaan direktris kurva di bawah ini adalah....

S10
Dari opsi jawaban berikut ini, manakah pernyataan yang salah mengenai kurva parabola di bawah ini?

