Contoh Soal Menggambar Kurva Ellips
Contoh Soal Menggambar Kurva Ellips - Pada topik sebelumnya, kalian telah belajar menganalisis data dan melakukan manipulasi aljabar pada masalah nyata mengenai ellips. Pada topik ini,kita akan belajar cara menggambar kurva ellips
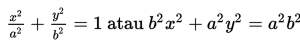
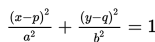
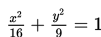
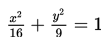
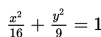
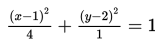
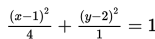

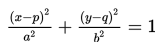
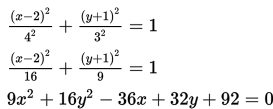
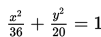
Mari kita simak langkah menggambar sketsa ellips
Langkah-langkah menggambar ellips adalah sebagai berikut :
1. Menentukan pusat ellips.
- Jika persamaanya berbentuk
Langkah-langkah menggambar ellips adalah sebagai berikut :
1. Menentukan pusat ellips.
- Jika persamaanya berbentuk
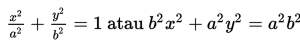
maka, ellips berpusat di (0,0)
- Jika persamaannya berbentuk
- Jika persamaannya berbentuk
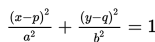
, ellips berpusat di (p,q).
Jika persamaannya berbentuk Ax2 + By2 + Cx + Dy + E = 0 ubah bentuknya menjadi seperti di atas dengan manipulasi aljabar, agar mudah menentukan pusatnya.
2. Menentukan letak fokus ellips (sumbu mayor) dan sumbu minor
Jika koordinat fokus ellips tidak disebutkan dalam soal, kalian bisa menentukan dimana letak fokusnya, sejajar sumbu x atau sejajar sumbu y. Sangat mudah membedakannya. Sumbu mayor ditandai dengan nilai a (karena panjang sumbu mayor = 2a), dengan catatan nilai a2 lebih besar dari nilai b2
- Jika a2 menjadi penyebut x2, fokus terletak pada sumbu x,
- Jika a2 menjadi penyebut (x – p)2, fokus terletak sejajar sumbu x,
- Jika a2 menjadi penyebut y2, fokus terletak pada sumbu y,
- Jika a2 menjadi penyebut (y – q)2, maka sumbu mayor sejajar sumbu y,
Perhatikan contoh berikut
Jika persamaannya berbentuk Ax2 + By2 + Cx + Dy + E = 0 ubah bentuknya menjadi seperti di atas dengan manipulasi aljabar, agar mudah menentukan pusatnya.
2. Menentukan letak fokus ellips (sumbu mayor) dan sumbu minor
Jika koordinat fokus ellips tidak disebutkan dalam soal, kalian bisa menentukan dimana letak fokusnya, sejajar sumbu x atau sejajar sumbu y. Sangat mudah membedakannya. Sumbu mayor ditandai dengan nilai a (karena panjang sumbu mayor = 2a), dengan catatan nilai a2 lebih besar dari nilai b2
- Jika a2 menjadi penyebut x2, fokus terletak pada sumbu x,
- Jika a2 menjadi penyebut (x – p)2, fokus terletak sejajar sumbu x,
- Jika a2 menjadi penyebut y2, fokus terletak pada sumbu y,
- Jika a2 menjadi penyebut (y – q)2, maka sumbu mayor sejajar sumbu y,
Perhatikan contoh berikut
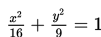
Pada ellips dengan persamaan di atas, sumbu mayor terletak di sumbu x
Dimana fokus berada, disitulah sumbu mayornya,kemudian buat sumbu lain tegak lurus dengan sumbu mayor dan melui titik pusat, yang kemudian disebut sumbu minor. Panjang kedua sumbu diatas adalah sebagai berikut :
Panjang sumbu mayor = 2a
Panjang sumbu minor = 2a
3. Menentukan puncak ellips
Puncak ellips berada di ujung –ujung sumbu mayor. Selain itu, tandai pula ujung-ujung sumbu minor
4. Hubungkan puncak ellips dan ujung-ujung sumbu minor dengan kurva lengkung, hingga membentuk ellips.
Dimana fokus berada, disitulah sumbu mayornya,kemudian buat sumbu lain tegak lurus dengan sumbu mayor dan melui titik pusat, yang kemudian disebut sumbu minor. Panjang kedua sumbu diatas adalah sebagai berikut :
Panjang sumbu mayor = 2a
Panjang sumbu minor = 2a
3. Menentukan puncak ellips
Puncak ellips berada di ujung –ujung sumbu mayor. Selain itu, tandai pula ujung-ujung sumbu minor
4. Hubungkan puncak ellips dan ujung-ujung sumbu minor dengan kurva lengkung, hingga membentuk ellips.
Agar lebih jelas memahami langkah menggambar sketsa sebuah ellips, mari kita lihat contoh berikut.
Contoh 1
Gambarlah ellips jika persamaannya adalah :
Gambarlah ellips jika persamaannya adalah :
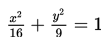
Solusi :
Berdasarkan persamaan, berikut hal-hal yang diketahui
Titik pusat (0,0)
a = 4
b = 3
Berdasarkan persamaan, berikut hal-hal yang diketahui
Titik pusat (0,0)
a = 4
b = 3
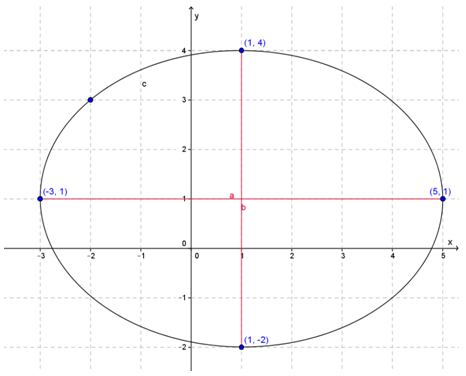
Sumbu mayor : sumbu x, panjang sumbu mayor = 2a = 8
Sumbu minor : sumbu y, panjang sumbu mayor = 2b = 6
Puncak : (-4,0) dan (4,0)
Ujung-ujung sumbu minor (0,-3) dan (0,3)
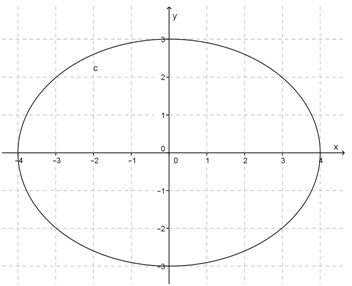
Setelah titik puncak dan ujung sumbu minor dihubungkan, berikut sketsa ellips
Sumbu minor : sumbu y, panjang sumbu mayor = 2b = 6
Puncak : (-4,0) dan (4,0)
Ujung-ujung sumbu minor (0,-3) dan (0,3)
Setelah titik puncak dan ujung sumbu minor dihubungkan, berikut sketsa ellips
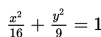

Contoh 2
Gambarlah grafik ellips jika diketahui persamaannya adalah:
Gambarlah grafik ellips jika diketahui persamaannya adalah:
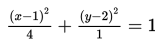
Solusi :
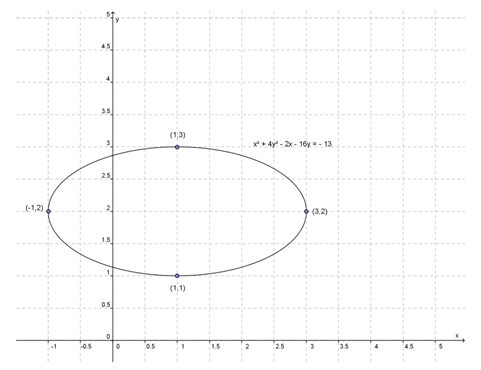
Berdasarkan persamaan, berikut hal-hal yang diketahui
Titik pusat (1,2)
a = 2
b = 1
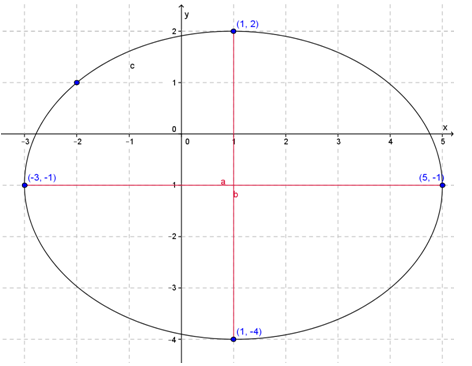
Sumbu mayor : sejajar sumbu x, panjang sumbu mayor = 2a = 4
Sumbu minor : sumbu y, panjang sumbu mayor = 2b = 2
Puncak : (-1,2) dan (3,2)
Ujung-ujung sumbu minor (1,1) dan (1,3)
Setelah titik puncak dan ujung sumbu minor dihubungkan, berikut sketsa ellips
Berdasarkan persamaan, berikut hal-hal yang diketahui
Titik pusat (1,2)
a = 2
b = 1
Sumbu mayor : sejajar sumbu x, panjang sumbu mayor = 2a = 4
Sumbu minor : sumbu y, panjang sumbu mayor = 2b = 2
Puncak : (-1,2) dan (3,2)
Ujung-ujung sumbu minor (1,1) dan (1,3)
Setelah titik puncak dan ujung sumbu minor dihubungkan, berikut sketsa ellips
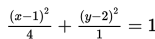

Contoh 3
Perhatikan gambar berikut ini.
Perhatikan gambar berikut ini.

Persamaan yang tepat untuk kurva di atas adalah ….
Solusi
Titik pusat ellips (2,-1), maka p = 2, q = -1
Panjang sumbu mayor = 2a = 8, a =4
Panjang sumbu minor = 2b = 6, b =3
Persamaan umum ellips =
Solusi
Titik pusat ellips (2,-1), maka p = 2, q = -1
Panjang sumbu mayor = 2a = 8, a =4
Panjang sumbu minor = 2b = 6, b =3
Persamaan umum ellips =
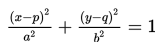
Maka persamaan ellips tersebut adalah :
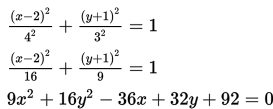
S1
Kurva ellips yang panjang sumbunya 26 dan 24 satuan, berpusat di (0,0), dan sumbu mayornya di x adalah …
S2
Sketsa ellips
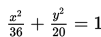
adalah ….
S3
Kurva ellips 25x2 + 49y2 = 1225 adalah …
S4
Kurva elips dengan pusat O (0, 0).Puncak (10, 0) dan (-10, 0) serta salah satu fokusnya (-6, 0) adalah ….
S5
Kurva ellips yang mungkin jika diketahui pusat di titik (0,0), panjang sumbu mayor dan minornya berturut-turut 16 dan 12 satuan panjang adalah ….
S6
Kurva ellips yang mungkin jika pusat (-1,1) dengan panjang sumbu 8 dan 6 satuan adalah ….
S7
Diketahui koordinat ujung sumbu mayor dan minor ellips berturut-turut adalah (-3,-1) dan (1,2); sumbu mayor sejajar sumbu x, dan berpusat di (1,-1). Sketsa ellips yang tepat adalah ….
S8
Kurva ellips dengan persamaan 4x2 + 9y2 – 24x – 36y + 36 = 0 adalah ….
S9

Persamaan yang tepat untuk kurva di atas adalah …
S10

Persamaan kurva di atas adalah …
