Contoh Soal Gelombang Berjalan

Contoh Soal Gelombang Berjalan - ada topik sebelumnya, kalian telah belajar tentang gelombang. Gelombang merupakan getaran yang merambat. Selama merambat, gelombang membawa energi tertentu dan melewati kedudukan tertentu pula. Karakteristik yang ada pada gelombang bersifat spesifik, contohnya panjang gelombang, amplitudo, frekuensi, dan lain sebagainya.

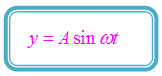
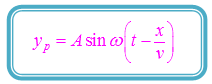
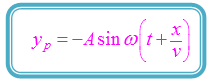
        Berdasarkan amplitudonya, gelombang dibagi menjadi dua, yaitu gelombang berjalan dan gelombang stasioner. Pada topik kali ini, kalian akan belajar tentang gelombang berjalan. Apa itu gelombang berjalan? Bagaimana terjadinya? Untuk mengetahuinya, mari simak topik ini dengan saksama.

☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳

Ambillah seutas tali. Peganglah salah satu ujungnya dan biarkan ujung lainnya bebas, tidak terikat. Kemudian gerakkan tali tersebut. Apa yang kalian lihat? Ya, kalian akan melihat gerakan tali menyerupai grafik sinus. Lantas, apakah gerakan tali tersebut akan memantul ketika sampai pada ujung yang lain? Ternyata tidak, tali akan tetap bergerak selama kalian menggerakkan ujung yang kalian pegang dan tali akan diam ketika kalian menghentikan gerakan tersebut.

        Salah satu alat yang dapat menggerakkan tali secara terus menerus adalah pegas. Ujung yang kalian pegang diganti oleh pegas yang terus berosilasi. Dengan begitu, tali akan terus bergerak dan membentuk sebuah gelombang. Gelombang yang dihasilkan pada tali inilah yang merupakan salah satu contoh gelombang berjalan.

☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳☳

🚶🚶🚶 KONSEP 🚶🚶🚶

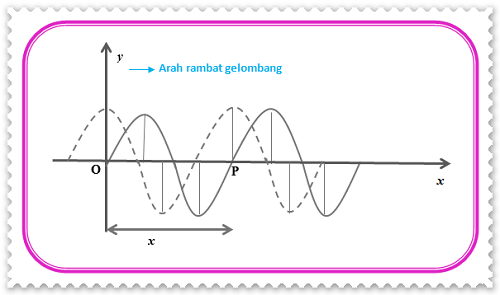
Gelombang berjalan adalah gelombang yang memiliki amplitudo yang sama di setiap titik. Jika kalian amati, tali yang digerakkan seperti penjelasan di awal topik ini tidak mengalami perubahan amplitudo. Oleh karena itu, keadaan tersebut akan menghasilkan gelombang berjalan dengan bentuk seperti berikut.

        Pada gambar di atas, terlihat bahwa gelombang merambat sejauh x m dari titik O ke titik P. Waktu yang dibutuhkan oleh gelombang untuk merambat dari titik O ke titik P adalah xv$\frac{x}{v}$ s. Persamaan simpangan gelombang di titik O dinyatakan sebagai berikut.

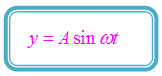
        Jika waktu yang dibutuhkan gelombang untuk bergetar di titik O adalah t s, maka waktu getar gelombang di titik P adalah (t−xv)$\left(t-\frac{x}{v}\right)$ s. Dengan demikian, persamaan gelombang di titik P dirumuskan sebagai berikut.

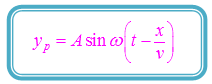
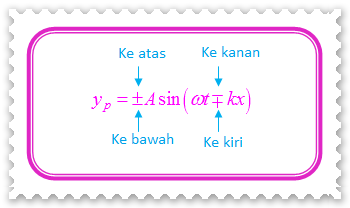
        Persamaan di atas berlaku jika gelombang merambat ke kanan--sumbu x positif-- dan bergetar ke atas. Jika gelombang merambat ke kiri--sumbu x negatif-- dan bergetar ke bawah, maka persamaannya menjadi seperti berikut.

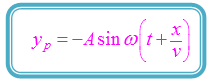
        Berdasarkan kedua persamaan di atas, diperoleh:

yp=±Asinω(t∓xv)yp=±Asin(ωt∓ωxv)yp=±Asin(ωt∓2πfxv)yp=±Asin(ωt∓x2πfv)yp=±Asin(ωt∓x2πλ)$\begin{array}{l}{y}_p=\pm A\sin \omega \left(t\mp \frac{x}{v}\right)\\ y_p=\pm A\sin \left(\omega t\mp \omega \frac{x}{v}\right)\\ y_p=\pm A\sin \left(\omega t\mp 2\pi f\frac{x}{v}\right)\\ y_p=\pm A\sin \left(\omega t\mp x\frac{2\pi f}{v}\right)\\ y_p=\pm A\sin \left(\omega t\mp x\frac{2\pi }{\lambda }\right)\end{array}$

Jadi, persamaan umum gelombang berjalan adalah sebagai berikut.

Keterangan:

yp = simpangan gelombang di titik P (m);

A = amplitudo gelombang (m);

ω = 2πf = 2πT$\frac{2\pi }{T}$ = kecepatan sudut gelombang (rad/s);

t = lamanya sumber getar bergetar (s);

k = 2πλ$\frac{2\pi }{\lambda }$ = bilangan gelombang (1, 2, 3, …); dan

x = kedudukan titik P (m).

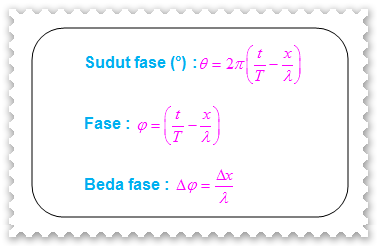
        Perhatikan kembali persamaan di atas. Sudut yang berada di dalam fungsi sinus disebut dengan sudut fase (dilambangkan dengan θ). Jadi, besar sudut fase di titik P adalah:

θ=ωt−kx=2πTt−2πλx=2π(tT−xλ)$\theta =\omega t-kx=\frac{2\pi }{T}t-\frac{2\pi }{\lambda }x=2\pi \left(\frac{t}{T}-\frac{x}{\lambda }\right)$

Sudut fase (θ) dapat kita tulis sebagai:

θ=2π(tT−xλ)=2πφ$\theta =2\pi \left(\frac{t}{T}-\frac{x}{\lambda }\right)=2\pi \phi$

dengan φ merupakan fase gelombang. Dengan demikian, fase gelombang di titik P adalah:

φ=(tT−xλ)$\phi =\left(\frac{t}{T}-\frac{x}{\lambda }\right)$

Jadi, beda fase antara dua titik yang berjarak x2 dan x1 dari sumber getar dapat dituliskan sebagai:

Δφ=(tT−x2λ)−(tT−x1λ)=−(x2−x1)λ=−Δxλ$\mathrm{\Delta }\phi =\left(\frac{t}{T}-\frac{x_2}{\lambda }\right)-\left(\frac{t}{T}-\frac{x_1}{\lambda }\right)=-\frac{(x_2-x_1)}{\lambda }=\frac{-\mathrm{\Delta }x}{\lambda }$.

Tanda negatif menunjukkan bahwa gelombang merambat ke kanan.

        Jika kalian ingin menentukan persamaan kecepatan dan percepatan gelombang di suatu titik, kalian cukup menurunkan dari persamaan simpangannya. Kecepatan gelombang merupakan turunan pertama dari simpangan gelombang, sedangkan percepatan gelombang merupakan turunan kedua dari simpangan gelombang.

SOAL 1

Perhatikan persamaan berikut.

y = A sin(ωt)

Besaran ωt disebut juga sebagai ….

SOAL 2

Gelombang yang memiliki amplitudo yang sama di setiap titik disebut ….

SOAL 3

Salah satu alat yang dapat digunakan untuk menggetarkan gelombang tali secara terus menerus adalah ….

SOAL 4

Suatu gelombang begerak dengan frekuensi 5 rad/s. Jika waktu getar gelombang di titik pusat adalah 3 s, maka sudut fasenya adalah …

SOAL 5

Gelombang tali memiliki persamaan gelombang seperti berikut.

y=5sin(π2t−πx)m$y=5\sin \left(\frac{\pi }{2}t-\pi x\right)\mathrm{m}$

Berdasarkan persamaan di atas, panjang gelombangnya adalah ….

SOAL 6

Perhatikan persamaan berikut.

y=sin(10πt−π5x)cm$y=\sin \left(10\pi t-\frac{\pi }{5}x\right)\mathrm{c}\mathrm{m}$

Cepat rambat gelombangnya adalah …

SOAL 7

Suatu tali digetarkan ke atas dengan amplitudo A dan getaran merambat dari titik O ke titik P ( ke arah sumbu x positif) dalam waktu 2 s. Jika frekuensi gelombang tersebut 5 Hz dan panjang gelombangnya 20 cm, maka persamaan gelombangnya adalah ….

SOAL 8

Suatu gelombang bergerak dengan persamaan berikut.

y=2sin(26πt+12x)m$y=2\sin \left(\frac{2}{6}\pi t+\frac{1}{2}x\right)\mathrm{m}$

Berdasarkan persamaan di atas, jarak antara dua puncak yang berdekatan adalah ….

SOAL 9

Gelombang yang bergerak menghasilkan persamaan berikut.

y=2sin(0,74t+4x)$y=2\sin \left(0,74t+4x\right)$

Arah gerak gelombang tersebut adalah ….

SOAL 10

Suatu gelombang berjalan memiliki persamaan berikut.

y=2sin2π(6t+23x)m$y=2\sin 2\pi \left(6t+\frac{2}{3}x\right)\mathrm{m}$

Jika saat t = 3 s kecepatan gelombangnya adalah 12π m/s, maka posisi gelombangnya berada pada x = ....

Share this post