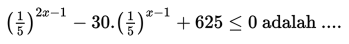Contoh Soal Pertidaksamaan Eksponen untuk a lebih dari 0 kurang dari 1

Contoh Soal Pertidaksamaan Eksponen untuk a lebih dari 0 kurang dari 1 - jika pada topik sebelumnya kalian telah belajar menyelesaikan pertidaksamaan eksponen untuk a > 1, maka pada topik kali ini kalian akan belajar menyelesaikan pertidaksamaan eksponen untuk 0 < a < 1. 

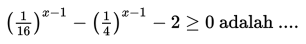
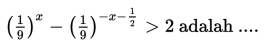
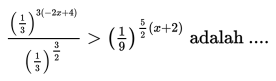
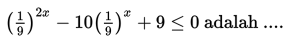
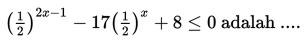
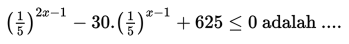
Grafik fungsi eksponen f(x) = ax untuk 0 < a < 1 memenuhi sifat-sifat berikut.

• merupakan fungsi monoton turun yang berarti untuk setiap x₁, x₂ ∈ R, berlaku x₁ < x₂ ⇔ f(x₁) > f(x₂)
• grafik memotong sumbu y di titik (0,1)
• grafik mempunyai daerah asal berupa himpunan semua bilangan real
• grafik mempunyai daerah hasil berupa himpunan bilangan real positif
• grafik mempunyai asimtot datar yaitu sumbu x
• fungsi selalu bernilai positif
• fungsi merupakan fungsi bijektif

Pada saat kalian belajar tentang sifat-sifat grafik fungsi eksponen f(x) = ax untuk 0 < a < 1, telah kalian ketahui bahwa untuk 0 < a < 1, fungsi f(x) = ax merupakan fungsi monoton turun. Hal ini berarti bahwa untuk setiap x₁, x₂ ∈ R, berlaku x₁ < x₂ ⇔ f(x₁) > f(x₂). Bagaimana jika sifat tersebut kita aplikasikan pada pertidaksamaan eksponen? Perhatikan penjelasan berikut.

Untuk 0 < a < 1

• af(x) ≥ ag(x) jika dan hanya jika f(x) ≤ g(x)
• af(x) ≤ ag(x) jika dan hanya jika f(x) ≥ g(x)

SOAL 1

Himpunan penyelesaian dari(15)3x+1<(125)2x+5${\left(\frac{1}{5}\right)}^{3x+1}<{\left(\frac{1}{25}\right)}^{2x+5}$ adalah ….

SOAL 2

Penyelesaian dari (23)2x>(278)5−2x${\left(\frac{2}{3}\right)}^{2x}>{\left(\frac{27}{8}\right)}^{5-2x}$ adalah ….

SOAL 3

Himpunan penyelesaian dari (14)2−x≤(12)3x+1−−−−−−√${\left(\frac{1}{4}\right)}^{2-x}\le \sqrt{{\left(\frac{1}{2}\right)}^{3x+1}}$ adalah ….

SOAL 4

Himpunan penyelesaian (14)2x2+3x−5≤64${\left(\frac{1}{4}\right)}^{2x^2+3x-5}\le 64$adalah ….

 SOAL 5

Nilai x yang memenuhi pertidaksamaan:

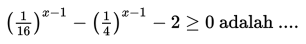
SOAL 6

Penyelesaian dari:

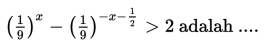
SOAL 7

Penyelesaian dari:

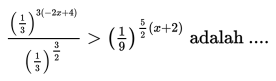
SOAL 8

Nilai x yang memenuhi pertidaksamaan:

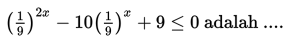
SOAL 9

Penyelesaian dari:

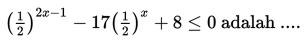
SOAL 10

Penyelesaian dari:

Share this post