Menghitung Panjang Diagonal Bidang
Menghitung Panjang Diagonal Bidang - Pada topik sebelumnya, kalian telah belajar tentang konsep dan sifat diagonal bidang. Nah, dalam topik kali ini, kalian akan belajar bagaimana cara menentukan panjang diagonal bidang.
Tahukah kalian bagaimana cara menentukan panjang ?
Berdasarkan uraian di atas, dapat disimpulkan bahwa panjang diagonal bidang kubus adalah jika panjang rusuk kubus adalah .
Penyelesaian:
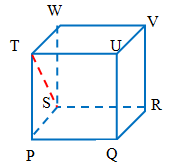
Materi di atas mudah dipahami bukan?
Nah, tahukah kalian bagaimana cara menentukan panjang diagonal bidang pada balok?
Agar kalian lebih jelas tentang bagaimana cara menentukan panjang diagonal bidang pada balok, yuk kita cermati contoh soal berikut.
Penyelesaian:
Oleh karena ruas garis terletak pada dengan titik siku adalah titik , maka
Oleh karena ruas garis terletak pada dengan titik siku adalah titik , maka
Nah, manakah yang dimaksud dengan diagonal bidang?
Penyelesaian:
Selanjutnya, karena bidang alas terdiri atas enam buah segitiga samasisi yang kongruen dengan titik pusat 60°, maka luas bidang alas dapat ditentukan sebagai berikut:
Jadi, luas bidang alas prisma tegak segienam beraturan adalah cm3.
Yuk kita cermati contoh berikut.
Penyelesaian:
Nah, sekarang kalian telah selesai mempelajari materi di atas.
 |
| Menghitung Panjang Diagonal Bidang |
Kubus
Seperti yang telah kalian ketahui, kubus mempunyai 12 diagonal bidang dengan panjang sama.
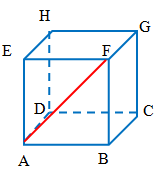
Nah, pada kubus , ruas garis merupakan diagonal bidang.

Tahukah kalian bagaimana cara menentukan panjang ?
Benar, kita dapat menentukan panjang dengan menggunakan teorema Pythagoras.
Oleh karena panjang dan siku-siku di titik , maka
Berdasarkan uraian di atas, dapat disimpulkan bahwa panjang diagonal bidang kubus adalah jika panjang rusuk kubus adalah .
Contoh 1
Diketahui panjang rusuk kubus adalah 5 cm. Hitung panjang ruas garis.
Penyelesaian:

Pada gambar di atas, tampak bahwa merupakan diagonal bidang .
Oleh karena panjang rusuk kubus adalah cm, maka panjang ruas garis adalah cm.
Materi di atas mudah dipahami bukan?
Balok
Sama halnya dengan kubus, balok juga mempunyai 12 diagonal bidang, hanya saja diagonal bidang pada balok berupa persegi panjang.
Nah, tahukah kalian bagaimana cara menentukan panjang diagonal bidang pada balok?
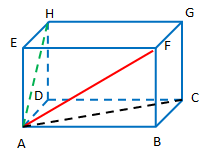
Yuk perhatikan gambar balok berikut.

Pada gambar di atas, tampak bahwa ada tiga kelompok panjang diagonal bidang pada balok. Nah, untuk menentukan panjang ketiga diagonal bidang tersebut, kalian dapat menggunakan rumus Pythagoras.
Agar kalian lebih jelas tentang bagaimana cara menentukan panjang diagonal bidang pada balok, yuk kita cermati contoh soal berikut.
Contoh 2
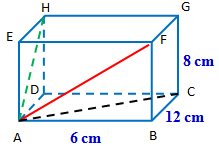
Diketahui balok dengan panjang rusuk , , dan berturut-turut adalah 6 cm, 12 cm, dan 8 cm. Tentukan panjang ruas garis , , dan .
Penyelesaian:

Oleh karena ruas garis terletak pada dengan titik siku adalah titik , maka
Oleh karena ruas garis terletak pada dengan titik siku adalah titik , maka
Oleh karena ruas garis terletak pada dengan titik siku adalah titik , maka
Prisma
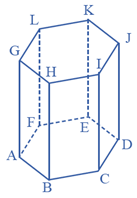
Perhatikan gambar prisma tegak segienam beraturan berikut.

Prisma tegak segienam pada gambar di atas mempunyai delapan sisi/bidang, yaitu
- → sisi alas
- → sisi atas
- , , , , , dan → sisi tegak
Nah, manakah yang dimaksud dengan diagonal bidang?
- Diagonal bidang pada bidang alas:
→ AC = AE = BF = BD= CE = DF
→ AD = BE = CF b. - Diagonal bidang pada bidang atas:
→ GI = GK = HL = HJ= IK = JL
→ GJ = HK = IL - Diagonal bidang pada bidang tegak:
→ BI = HC =DI = CJ = DK = EJ = EL = FK = AL = FG = AH = BG
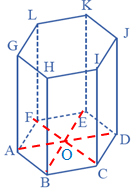
Contoh 3
Diketahui prisma tegak segienam beraturan dengan panjang adalah 24 cm. Tentukan luas bidang alas .
Penyelesaian:

Oleh karena alas prisma berupa segienam beraturan, maka diagonal bidang alas berpotongan sama panjang.
Akibatnya, cm.
Selanjutnya, karena bidang alas terdiri atas enam buah segitiga samasisi yang kongruen dengan titik pusat 60°, maka luas bidang alas dapat ditentukan sebagai berikut:
Jadi, luas bidang alas prisma tegak segienam beraturan adalah cm3.
Limas
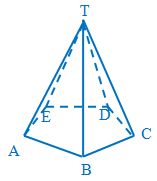
Apakah kalian masih ingat dengan sifat dari limas segilima beraturan?

Pada gambar di atas, tampak bahwa limas segilima beraturan mempunyai lima diagonal bidang. Adapun diagonal bidang tersebut terletak pada bidang alas.
Seperti yang kalian pelajari pada topik sebelumnya, panjang kelima diagonal bidang adalah sama → .
Yuk kita cermati contoh berikut.
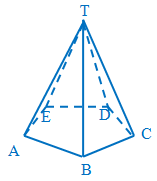
Contoh 4
Diketahui limas segilima beraturan dengan panjang adalah 4 cm. Tentukan panjang diagonal bidang .
Penyelesaian:

Oleh karena panjang diagonal bidang pada limas adalah sama panjang, maka cm.
Oleh karena diagonal bidang pada alas berpotongan di satu titik sedemikian hingga terbentuk lima buah segitiga sama kaki dengan sudut pusat 72°, maka .
Selanjutnya, jika kita gunakan aturan kosinus, maka kita peroleh hubungan sebagai berikut:
Nah, karena , maka panjang diagonal bidang adalah 6,47 cm.
Nah, sekarang kalian telah selesai mempelajari materi di atas.