Konsep dan Sifat Diagonal Bidang
Konsep dan Sifat Diagonal Bidang - Coba kalian perhatikan barang-barang yang ada di sekitar kalian. Kotak kapur, kardus makanan, korek api, dan adaptor laptop berbentuk balok. Permen coklat ada yang berbentuk prisma segiempat. Bentuk botol minyak wangi ada yang berbentuk balok, limas segitiga, bola, maupun tabung.
Nah, sekarang coba identifikasi nama bangun ruang pada gambar berikut.

Yuk kita pelajari konsep dan sifat diagonal bidang dari keempat bangun ruang tersebut.
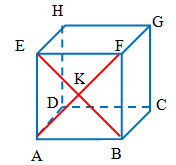
Tahukah kalian diagonal bidang selain AF dalam kubus di atas?
Tahukah kalian sifat-sifat diagonal bidang pada kubus?
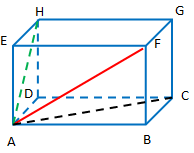
Apakah kalian masih ingat dengan definisi balok?
Jika kalian perhatikan, ruas garis menghubungkan dua titik sudut yang saling berhadapan pada satu bidang, yaitu titik dan . Nah, ruas garis yang mempunyai sifat seperti garis dinamakan diagonal bidang dari balok .
Tahukah kalian digaonal bidang selain dalam kubus ABCD.EFGH di atas?
Nah, bagaimanakah sifat-sifat diagonal bidang pada balok?
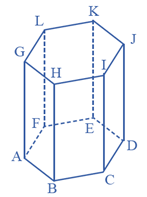
Selanjutnya, jika kita perhatikan ruas garis , ternyata terletak pada sisi tegak yang ditarik dari dua titik sudut yang saling berhadapan.
Adakah yang tahu bagaimana sifat-sifat diagonal bidang pada prisma segi- beraturan?
Selanjtnya, karena
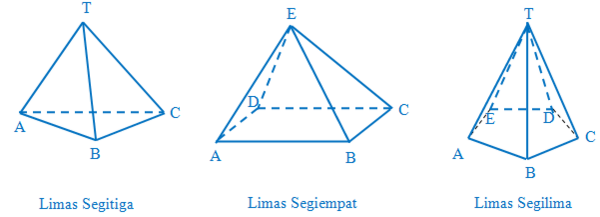
Apakah kalian masih ingat dengan definisi diagonal bidang?
Apa yang dapat kalian simpulkan mengenai banyak diagonal bidang pada limas segi-?
Nah, kalian sudah selesai mempelajari materi dalam topik ini.
Yuk kerjakan sepuluh latihan soal dalam topik ini.
 |
| Konsep dan Sifat Diagonal Bidang |
Nah, sekarang coba identifikasi nama bangun ruang pada gambar berikut.

Ya, nama bangun ruang dari gambar a, b, c, dan d berturut-turut adalah kubus, balok, prisma segi-4 beraturan, dan limas segitiga.
Yuk kita pelajari konsep dan sifat diagonal bidang dari keempat bangun ruang tersebut.
Kubus
Sisi kubus merupakan bidang yang membatasi kubus. Seperti yang telah kalian ketahui, semua sisi kubus berbentuk persegi dan semua rusuknya sama panjang.

Pada gambar di atas, adalah sisi alas, adalah sisi atas, sedangkan , , , dan merupakan sisi tegak.
Nah, sekarang coba kalian perhatikan garis pada kubus ABCD.EFGH di atas.
Tampak bahwa garis menghubungkan dua titik sudut yang saling berhadapan dalam satu sisi kubus. Lebih lanjut, garis dinamakan diagonal sisi atau diagonal bidang.
Tahukah kalian diagonal bidang selain AF dalam kubus di atas?
Ya, diagonal bidang yang lain adalah , , , , , , , , , , dan .
Dengan demikian, kubus memiliki 12 diagonal bidang.
Tahukah kalian sifat-sifat diagonal bidang pada kubus?
Ya, diagonal bidang pada kubus mempunyai tiga sifat sebagai berikut:
- diagonal bidang kubus sama panjang →
- dua diagonal bidang yang terletak dalam satu bidang akan berpotongan ditengah-tengah dan saling tegak lurus → contoh: dan
- ada tiga diagonal bidang yang bertemu pada setiap titik sudut → contoh: , , dan bertemu pada titik sudut A
Balok
Perhatikan kotak kapur di kelasmu.
Secara geometris, sketsa kotak kapur tersebut adalah sebagai berikut.

Nah, bangun di atas dinamakan balok .
Apakah kalian masih ingat dengan definisi balok?
Ya, balok adalah bangun ruang yang memiliki tiga pasang sisi berhadapan yang sama bentuk dan ukurannya, dimana setiap sisinya berbentuk persegipanjang.
Jika kalian perhatikan, ruas garis menghubungkan dua titik sudut yang saling berhadapan pada satu bidang, yaitu titik dan . Nah, ruas garis yang mempunyai sifat seperti garis dinamakan diagonal bidang dari balok .
Tahukah kalian digaonal bidang selain dalam kubus ABCD.EFGH di atas?
Ya, diagonal bidang yang lain adalah , , , , , , , , , , dan .
Dengan demikian, balok mempunyai 12 diagonal bidang.
Nah, bagaimanakah sifat-sifat diagonal bidang pada balok?
Ya, diagonal bidang pada balok mempunyai tiga sifat sebagai berikut:
- ada tiga kelompok diagonal bidang yang sama panjang → , ,
- dua diagonal bidang yang terletak dalam satu bidang akan berpotongan ditengah-tengah dan saling tegak lurus → contoh: dan
- ada tiga diagonal bidang yang bertemu pada setiap titik sudut → contoh: , , dan bertemu pada titik sudut A
Prisma
Coba perhatikan pensil 2B kalian yang belum kalian raut. Secara geometris, sketsa dari pensil 2B tersebut berupa prisma segi-6 beraturan.

Jika kalian perhatikan sketsa di atas, tampak bahwa bentuk alas dan atap adalah kongruen (sama dan sebangun) dan semua sisi pada bagian dinding berbentuk persegipanjang dan kongruen.
Nah, berdasarkan bangun di atas, dapat kita simpulkan bahwa prisma segi-6 beraturan mempunyai 8 sisi (bidang), yaitu sisi alas , sisi atas , dan sisi tegak , , , , , dan .
Perlu kalian ketahui, sisi tegak dari prisma segi-6 berbentuk persegi panjang yang kongruen.
Selanjutnya, jika kita perhatikan ruas garis , ternyata terletak pada sisi tegak yang ditarik dari dua titik sudut yang saling berhadapan.
Nah, ruas garis seperti itu selanjutnya disebut diagonal bidang.
Adakah yang tahu bagaimana sifat-sifat diagonal bidang pada prisma segi- beraturan?
Jika kita perhatikan prisma ABCDEF.GHIJKL di atas, maka dapat kita simpulkan bahwa sifat-sifat diagonal bidang pada prisma segi-6 adalah sebagai berikut:
- diagonal bidang pada bidang alas sama panjang → banyak diagonal bidang pada bidang alas dari prisma segi-6 adalah
- diagonal bidang pada bidang atas sama panjang → banyak diagonal bidang pada bidang atas dari prisma segi-6 adalah
- ada enam bidang tegak berupa persegi panjang yang kongruen → ada diagonal bidang pada bidang tegak
Dengan demikian, ada 30 diagonal bidang pada prisma segi-6 beraturan.
Selanjtnya, karena
- banyak diagonal bidang pada prisma segi-3 beraturan adalah 6 = 3 x 2
- banyak diagonal bidang pada prisma segi-4 beraturan adalah 12 = 4 x 3
- banyak diagonal bidang pada prisma segi-5 beraturan adalah 20 = 5 x 4
- banyak diagonal bidang pada prisma segi-6 beraturan adalah 30 = 6 x 5
maka dapat kita simpulkan bahwa banyak diagonal bidang pada prisma segi-beraturan adalah .
Limas
Apakah kalian pernah melihat gambar piramida di Mesir?
Pasti kalian semua sudah pernah melihatnya.
Nah, apa sebutan lain untuk piramida?
Benar, namanya adalah limas segi empat beraturan. Bangun ruang tersebut mempunyai lima sisi berupa segitiga dan sebuah titik puncak.

Jika kalian perhatikan gambar di atas, terlihat bahwa setiap limas memiliki sisi tegak berbentuk segitiga.
Nah, pada limas segiempat , sisi yang terbentuk adalah sisi alas dan sisi tegak , , , dan .
Apakah kalian masih ingat dengan definisi diagonal bidang?
Ya, diagonal bidang adalah ruas garis menghubungkan dua titik sudut yang saling berhadapan dalam satu sisi.
Yuk kita hitung banyak diagonal bidang dari limas dengan memperhatikan gambar di atas.
- banyak diagonal imas segitiga adalah nol →
- banyak diagonal imas segiempat adalah dua →
- banyak diagonal imas segilima adalah lima →
- banyak diagonal imas segienam adalah sembilan →
Apa yang dapat kalian simpulkan mengenai banyak diagonal bidang pada limas segi-?
Berdasarkan pola pada uraian di atas, dapat kita simpulkan bahwa banyak diagonal bidang pada limas segi- adalah .
Nah, kalian sudah selesai mempelajari materi dalam topik ini.
Yuk kerjakan sepuluh latihan soal dalam topik ini.