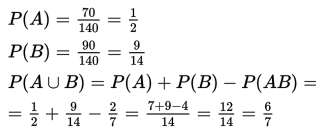Peluang dari Tabel Dua Arah
Peluang dari Tabel Dua Arah - Ketika mengerjakan materi mengenai peluang, kita akan menghadapi banyak data. Dalam hal ini, kita dapat menggunakan tabel dwi-arah untuk menyusun data tersebut. Akan berguna bila mempunyai 2 variabel yang mungkin mempunyai beberapa nilai.
Ke dalam tabel, kita dapat memasukkan semua kejadian dan frekuensi percobaannya.
Contoh:
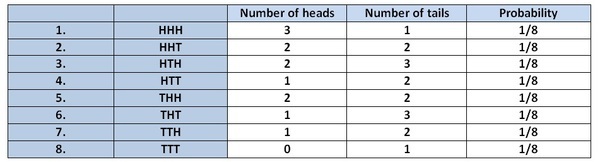
Kita melempar sekeping koin 3 kali. Semua hasil yang mungkin adalah:
Ω ={KKK, KKE, KEK, KEE, EKK, EKE, EEK, EEE}.
Jadi, terdapat 8 kemungkinan hasil. Selanjutnya, mari kita buat sebuah tabel dwi-arah:
a) a) Berapakah peluang munculnya paling kurang 1 kepala (K) dalam kejadian ini?
Mari kita lihat tabel di atas: Ada 7 hasil dengan paling sedikit satu kepala.
Jika kita tandai dengan D untuk kejadian munculnya paling kurang satu kepala, maka kita akan memperoleh peluang kejadian D sebagai berikut:
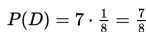
b) b) Berapakah peluang munculnya paling sedikit dua kepala dan satu ekor?
Mari kita periksa kembali tabelnya: Hasil-hasilnya terdapat dalam nomor 1, 2, 3, 5. Jadi, ada 4 hasil.
Jika kita tandai kejadian ini dengan F, maka kita peroleh peluangnya di bawah ini:
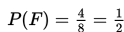
Contoh:
Mari kita lihat tabel dwi-arah yang tersedia:
A’ adalah komplemen kejadian A, demikian pula kejadian B’.
Data kita tersedia dalam angka-angka berwarna hitam.
Berapakah mean angka-angka tersebut?
Dalam kolom B dan baris A, terdapat angka 40. Ini berarti bahwa ada 40 elemen dalam irisan kejadian A and B (A∩B). Demikian pula terlihat adanya 30 elemen dalam interseksi kejadian A dan B’, 50 dalam A’∩B, dan 20 dalam kejadian A’∩B’.
Sekarang kita dapat menghitung jumlah total elemen (angka merah) dalam kejadian B; yaitu 90, dan dalam kejadian B' ada 50 elemen. Dengan menerapkan penghitungan yang sama, kita mendapat 70 elemen baik dalam kejadian A maupun A'.
Jadi, seluruhnya ada 140 elemen.
Dengan demikian, kita dapat pula memasukkan peluang-peluangnya ke dalam tabel yang sama sebagai ganti jumlah elemen.
Mari kita tuliskan peluang-peluangnya seperti di bawah ini:
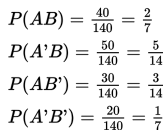
Dengan demikian sekarang kita dapat mencari peluang gabungan kejadian A dan B dengan cara sebagai berikut:
 |
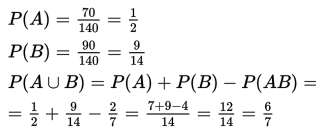
| Peluang dari Tabel Dua Arah |
Ke dalam tabel, kita dapat memasukkan semua kejadian dan frekuensi percobaannya.
Contoh:
Kita melempar sekeping koin 3 kali. Semua hasil yang mungkin adalah:
Ω ={KKK, KKE, KEK, KEE, EKK, EKE, EEK, EEE}.
Jadi, terdapat 8 kemungkinan hasil. Selanjutnya, mari kita buat sebuah tabel dwi-arah:
a) a) Berapakah peluang munculnya paling kurang 1 kepala (K) dalam kejadian ini?
Mari kita lihat tabel di atas: Ada 7 hasil dengan paling sedikit satu kepala.
Jika kita tandai dengan D untuk kejadian munculnya paling kurang satu kepala, maka kita akan memperoleh peluang kejadian D sebagai berikut:
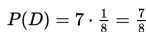
b) b) Berapakah peluang munculnya paling sedikit dua kepala dan satu ekor?
Mari kita periksa kembali tabelnya: Hasil-hasilnya terdapat dalam nomor 1, 2, 3, 5. Jadi, ada 4 hasil.
Jika kita tandai kejadian ini dengan F, maka kita peroleh peluangnya di bawah ini:
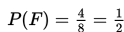
Contoh:
Mari kita lihat tabel dwi-arah yang tersedia:
A’ adalah komplemen kejadian A, demikian pula kejadian B’.
Data kita tersedia dalam angka-angka berwarna hitam.
Berapakah mean angka-angka tersebut?
Dalam kolom B dan baris A, terdapat angka 40. Ini berarti bahwa ada 40 elemen dalam irisan kejadian A and B (A∩B). Demikian pula terlihat adanya 30 elemen dalam interseksi kejadian A dan B’, 50 dalam A’∩B, dan 20 dalam kejadian A’∩B’.
Sekarang kita dapat menghitung jumlah total elemen (angka merah) dalam kejadian B; yaitu 90, dan dalam kejadian B' ada 50 elemen. Dengan menerapkan penghitungan yang sama, kita mendapat 70 elemen baik dalam kejadian A maupun A'.
Jadi, seluruhnya ada 140 elemen.
Dengan demikian, kita dapat pula memasukkan peluang-peluangnya ke dalam tabel yang sama sebagai ganti jumlah elemen.
Mari kita tuliskan peluang-peluangnya seperti di bawah ini:
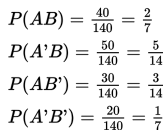
Dengan demikian sekarang kita dapat mencari peluang gabungan kejadian A dan B dengan cara sebagai berikut: