Invers Matriks 2 x 2

Invers Matriks 2 x 2 - Pada topik sebelumnya, kalian telah belajar tentang determinan matriks ordo 2 x 2. Pada topik kali ini, kalian akan belajar tentang invers matriksnya. Dalam matematika, invers diartikan sebagai balikan atau kebalikan. Misalnya, invers dari 2 adalah kebalikan dari 2, yaitu 

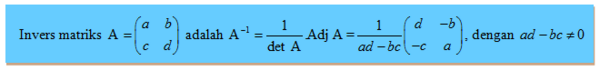
12$\frac{1}{2}$, invers dari 3 adalah kebalikan dari 3, yaitu 13$\frac{1}{3}$. Lantas, bagaimana cara menentukan invers suatu matriks? Apakah sama seperti invers suatu bilangan? Untuk mengetahuinya, mari kita pelajari bersama.

Invers Matriks 2 x 2

🏠 KONSEP

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

Misalkan A dan B adalah matriks persegi berordo sama dan berlaku AB = BA = I dengan I adalah matriks identitas, maka B disebut invers dari A dan A disebut invers dari B. Dengan kata lain, A dan B saling invers. Invers dari matriks A disimbolkan dengan A-1 , sedangkan invers dari matriks B disimbolkan dengan B-1 .

Berikut ini merupakan penjelasan tentang cara menentukan invers matriks persegi berordo dua, yaitu sebagai berikut.

Misalkan matriks A=(acbd)$\mathrm{A}=\left(\begin{array}{ll}a& b\\ c& d\end{array}\right)$ dan invers matriks A adalah A−1=(xuyv)${\mathrm{A}}^{-1}=\left(\begin{array}{ll}x& y\\ u& v\end{array}\right)$ .

Oleh karena A dan A-1 saling invers, maka berlaku AA-1 = I.

AA−1⇔(acbd)(xuyv)⇔(ax+bucx+duay+bvcy+dv)===I(1001)(1001)$\begin{array}{lll}\mathrm{A}{\mathrm{A}}^{-1}& =& \mathrm{I}\\ \iff \left(\begin{array}{ll}a& b\\ c& d\end{array}\right)\left(\begin{array}{ll}x& y\\ u& v\end{array}\right)& =& \left(\begin{array}{ll}1& 0\\ 0& 1\end{array}\right)\\ \iff \end{array}$

$\begin{array}{lll}\left(\begin{array}{ll}ax+bu& ay+bv\\ cx+du& cy+dv\end{array}\right)& =& \left(\begin{array}{ll}1& 0\\ 0& 1\end{array}\right)\end{array}$

Berdasarkan kesamaan matriks, diperoleh:

ax+bu=1…(1)cx+du=0…(2)ay+bv=0…(3)cy+dv=1…(4)$\begin{array}{l}ax+bu=1\dots \left(1\right)\\ cx+du=0\dots \left(2\right)\\ ay+bv=0\dots \left(3\right)\\ cy+dv=1\dots \left(4\right)\end{array}$

Selanjutnya, mari kita selesaikan sistem persamaan tersebut untuk menentukan nilai x, y, u, dan v.

ax+bu=1cx+du=0∣∣∣×d×b∣∣∣adx+bdu=dbcx+bdu=0⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯adx−bcx=d$\begin{array}{l}\begin{array}{l}ax+bu=1\\ cx+du=0\end{array}|\begin{array}{l}\times d\\ \times b\end{array}|\underset{}{\begin{array}{l}adx+bdu=\end{array}}\end{array}$

$\begin{array}{l}\underset{\_}{\begin{array}{l}d\\ bcx+bdu=0\end{array}}\\ adx-bcx=d\end{array}$

Dengan demikian, di dapatkan:

adx−bcx(ad−bc)xx===dddad−bc$\begin{array}{lll}adx-bcx& =& d\\ \left(ad-bc\right)x& =& d\\ x& =& \frac{d}{ad-bc}\end{array}$

Substitusikan nilai x pada persamaan (1), sehingga diperoleh:

ax+bua(dad−bc)+buadad−bc+bubububuu=======1111−adad−bcad−bcad−bc−adad−bc−bcad−bc−cad−bc$\begin{array}{lll}ax+bu& =& 1\\ a\left(\frac{d}{ad-bc}\right)+bu& =& 1\\ \frac{ad}{ad-bc}+bu& =& 1\\ bu& =\end{array}$

$\begin{array}{l}1-\frac{ad}{ad-bc}\\ bu& =& \frac{ad-bc}{ad-bc}-\frac{ad}{ad-bc}\\ bu& =& -\frac{bc}{ad-bc}\\ u& =& -\frac{c}{ad-bc}\end{array}$

Dengan cara yang sama seperti di atas, akan diperoleh juga:

y=−bad−bc$y=\frac{-b}{ad-bc}$

v=aad−bc$v=\frac{a}{ad-bc}$

Dengan demikian, komponen invers matriks A dapat dituliskan sebagai berikut:

A−1=(xuyv)=(dad−bc−cad−bc−bad−bcaad−bc)=1ad−bc(d−c−ba), dengan ad−bc≠0$\begin{array}{ll}{\mathrm{A}}^{-1}& =\left(\begin{array}{ll}x& y\\ u& v\end{array}\right)\\ & =(\begin{array}{ll}\frac{d}{ad-bc}& \frac{-b}{ad-bc}\\ \frac{-}{}\end{array}\end{array}$

$\begin{array}{l}\begin{array}{ll}\frac{c}{ad-bc}& \frac{a}{ad-bc}\end{array})\\ & =\frac{1}{ad-bc}\left(\begin{array}{ll}d& -b\\ -c& a\end{array}\right),\text{ dengan }ad-bc\ne 0\end{array}$

Dari uraian di atas, dapat disimpukan sebagai berikut:

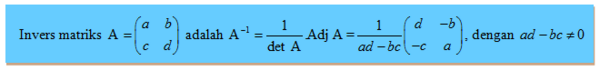
Dari definisi di atas, dapat diketahui syarat suatu matriks A agar mempunyai invers.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

• Jika det A = 0 atau ad - bc = 0, maka pembagian tersebut tidak terdefinisikan, sehingga A tidak mempunyai invers. Matriks yang tidak mempunyai invers disebut matriks singular.
• Jika det A ≠ 0 atau ad - bc ≠ 0, maka matriks A mempunyai invers. Matriks yang mempunyai invers disebut matriks nonsingular.

▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩▩

        Apakah kalian sudah paham tentang definisi invers matriks di atas? Jika sudah, mari kita cari tahu hubungan invers ini dengan transpos dan determinan dari suatu matriks yang telah kita pelajari sebelumnya.

Diketahui:

A=(acbd)$\mathrm{A}=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$

Invers dari A adalah:

A−1=1ad−bc(d−c−ba)=1det(A)(d−c−ba)$\begin{array}{ll}{\mathrm{A}}^{-1}& =\frac{1}{ad-bc}\left(\begin{array}{ll}d& -b\\ -c& a\end{array}\right)\\ & =\frac{1}{det\left(A\right)}\left(\begin{array}{ll}d& -b\\ -c& a\end{array}\right)\end{array}$

Lalu, bagaimana dengan invers dari AT ?

Nilai dari AT adalah:

AT=(abcd)${\mathrm{A}}^{\mathrm{T}}=\left(\begin{array}{ll}a& c\\ b& d\end{array}\right)$

Dengan demikian, diperoleh:

(AT)−1=1ad−bc(d−b−ca)=1det(A)(d−b−ca)=1det(A)(d−c−ba)T$\begin{array}{ll}{\left({\mathrm{A}}^{\mathrm{T}}\right)}^{-1}& =\frac{1}{ad-bc}\left(\begin{array}{ll}d& -c\\ -b& a\end{array}\right)\\ & =\frac{1}{det\left(\mathrm{A}\right)}\left(\begin{array}{ll}d& -c\\ -b& a\end{array}\right)\\ & =\end{array}$

$\begin{array}{l}\frac{1}{det\left(\mathrm{A}\right)}{\left(\begin{array}{ll}d& -b\\ -c& a\end{array}\right)}^{\mathrm{T}}\end{array}$

Jadi, (AT)−1=(A−1)T$({\mathrm{A}}^{\mathrm{T}}{)}^{-1}=({\mathrm{A}}^{-1}{)}^{\mathrm{T}}$ .

Selain sifat di atas, masih ada beberapa sifat yang berhubungan dengan invers matriks berikut ini.

☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲

Jika A dan B adalah matriks nonsingular, maka berlaku:

𝓪. AA−1=A−1A=I$\mathrm{A}{\mathrm{A}}^{-1}={\mathrm{A}}^{-1}\mathrm{A}=\mathrm{I}$

𝓫. (A−1)−1=A$({\mathrm{A}}^{-1}{)}^{-1}=\mathrm{A}$

𝓬. (A.B)−1=B−1.A−1${\left(\mathrm{A}.\mathrm{B}\right)}^{-1}={\mathrm{B}}^{-1}.{\mathrm{A}}^{-1}$

𝓭. (AT)−1=(A−1)T$({\mathrm{A}}^{\mathrm{T}}{)}^{-1}=({\mathrm{A}}^{-1}{)}^{\mathrm{T}}$

☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲☲

Contoh 1

Tentukan invers matriks berikut.

A=(2−2−15)$\mathrm{A}=\left(\begin{array}{ll}2& -1\\ -2& 5\end{array}\right)$

Jawab:

Invers matriks A=(acbd)$\mathrm{A}=\left(\begin{array}{ll}a& b\\ c& d\end{array}\right)$ adalah A−1=1ad−bc(d−c−ba)${\mathrm{A}}^{-1}=\frac{1}{ad-bc}\left(\begin{array}{ll}d& -b\\ -c& a\end{array}\right)$.

Dengan demikian, invers matriks A=(2−2−15)$\mathrm{A}=\left(\begin{array}{ll}2& -1\\ -2& 5\end{array}\right)$ adalah:

A−1=1(2.5)−(−1.−2)(5212)=110−2(5212)=18(5212)=(58281828)$\begin{array}{ll}{\mathrm{A}}^{-1}& =\frac{1}{\left(2.5\right)-\left(-1.-2\right)}\left(\begin{array}{ll}5& 1\\ 2& 2\end{array}\right)\\ & =\frac{1}{10-2}\left(\begin{array}{ll}5& 1\\ 2& 2\end{array}\right)\\ & =\end{array}$

$\begin{array}{l}\frac{1}{8}\left(\begin{array}{ll}5& 1\\ 2& 2\end{array}\right)\\ & =\left(\begin{array}{ll}\frac{5}{8}& \frac{1}{8}\\ \frac{2}{8}& \frac{2}{8}\end{array}\right)\end{array}$

Contoh 2

Diketahui A=(1533)$\mathrm{A}=\left(\begin{array}{ll}1& 3\\ 5& 3\end{array}\right)$ dan I=(1001)$\mathrm{I}=\left(\begin{array}{ll}1& 0\\ 0& 1\end{array}\right)$ . Tentukan nilai k jika matriks (A - kI) adalah matriks singular.

Jawab:

Misalkan P = (A - kI), maka:

P=(A−kI)=((1533)−k(1001))=((1533)−(k00k))=(1−k533−k)$\begin{array}{ll}\mathrm{P}& =\left(\mathrm{A}-k\mathrm{I}\right)\\ & =\left(\left(\begin{array}{ll}1& 3\\ 5& 3\end{array}\right)-k\left(\begin{array}{ll}1& 0\\ 0& 1\end{array}\right)\right)\\ & =\left(\left(\begin{array}{ll}1& 3\\ 5& 3\end{array}\right)-\left(\begin{array}{ll}k& 0\\ 0& k\end{array}\right)\right)\\ & =\left(\begin{array}{ll}1-k& 3\\ 5& 3-k\end{array}\right)\end{array}$

Oleh karena P matriks singular, maka det (P) = 0, sehingga diperoleh:

det(P)(1−k)(3−k)−(3.5)3−k−3k+k2−15k2−4k−12(k+2)(k−6)k=−2 atau k=6=====00000$\begin{array}{lll}det\left(\mathrm{P}\right)& =& 0\\ \left(1-k\right)\left(3-k\right)-\left(3.5\right)& =& 0\\ 3-k-3k+k^2-15& =\end{array}$

$\begin{array}{l}0\\ k^2-4k-12& =& 0\\ \left(k+2\right)\left(k-6\right)& =& 0\\ k=-2\text{ atau }k=6\end{array}$

Jadi, nilai k adalah -2 atau 6.

Nah, kalian telah selesai belajar tentang invers matriks ordo 2 x 2. Sekarang, saatnya kalian mengasah pemahaman dengan mengerjakan latihan soal-soal berikut. Selamat berlatih.

Share this post