Contoh Soal Menyelesaikan SPLDV dengan Metode Eliminasi
Contoh Soal Menyelesaikan SPLDV dengan Metode Eliminasi - Pada topik sebelumnya sempat disinggung bahwa sistem persamaan linear dua varibel juga dapat diselesaikan dengan metode eliminasi.
Yuk kita cari tahu bagaimana cara menyelesaikan SPLDV dengan metode eliminasi dari beberapa contoh soal berikut.
Penyelesaian:
Langkah pertama adalah memodelkan permasalahan dalam soal.
Langkah kedua adalah mengeliminasi variabel .
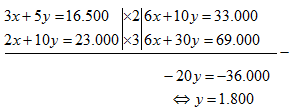
Langkah ketiga adalah mengeliminasi variabel .
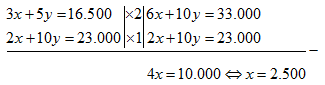
Berdasarkan hasil pada langkah kedua dan ketiga, dapat kita simpulkan bahwa harga segelas es teh adalah Rp2.500,00, sedangkan harga secangkir kopo panas adalah Rp1.800,00.
Penyelesaian:
Oleh karena koefisien variabel dan pada kedua persamaan adalah sama, maka
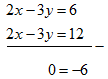
Nah, tahukah kalian apa arti dari eliminasi?
Dalam istilah matematika, eliminasi adalah menghilangkan salah satu variabel bebas, sehingga nilai variabel yang lain dapat ditentukan.
Yuk kita cari tahu bagaimana cara menyelesaikan SPLDV dengan metode eliminasi dari beberapa contoh soal berikut.
Contoh 1
Suatu hari Arya, Panji, dan Galuh pergi ke sebuah warung untuk mentraktir teman-temannya. Arya memesan 3 gelas es teh dan 5 cangkir kopi panas dengan harga Rp16.500,00, sedangkan Panji memesan 2 gelas es teh dan 10 cangkir kopi panas dengan harga Rp23.000,00. Jika Galuh juga ingin ikut berpartisipasi untuk mentraktir teman-temannya dengan memesan 5 gelas es teh dan 6 cangkir kopi panas, maka berapakah yang harus dibayar oleh Galuh?
Penyelesaian:
Langkah pertama adalah memodelkan permasalahan dalam soal.
Misal:
- harga segelas es teh adalah
- harga secangkir kopi panas adalah
Model matematika dari permasalahan dalam soal adalah .
Langkah kedua adalah mengeliminasi variabel .
Agar variabel dari kedua persamaan hilang, maka koefisien dari variabel pada kedua persamaan haruslah sama.
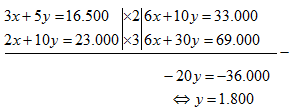
Langkah ketiga adalah mengeliminasi variabel .
Agar variabel dari kedua persamaan hilang, maka koefisien dari variabel pada kedua persamaan haruslah sama.
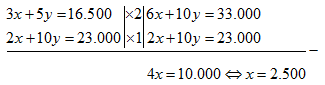
Berdasarkan hasil pada langkah kedua dan ketiga, dapat kita simpulkan bahwa harga segelas es teh adalah Rp2.500,00, sedangkan harga secangkir kopo panas adalah Rp1.800,00.
Oleh karena Galuh memesan 5 gelas es teh dan 6 cangkir kopi panas, maka Galuh harus membayar sebesar 5(Rp2.500,00) + 6(Rp1.800,00) = Rp23.300,00.
Contoh 2
Tentukan penyelesaian dari SPLDV: .
Penyelesaian:
Oleh karena koefisien variabel dan pada kedua persamaan adalah sama, maka
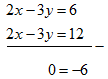
Jika kita perhatikan, penyelesaian di atas sangat tidak mungkin, sebab 0 ≠ -6.
Dengan demikian, SPLDV: tidak mempunyai penyelesaian.
S1
Penyelesaian dari SPLDV: adalah ....
S2
Penyelesaian dari SPLDV: adalah ....
S3
Penyelesaian dari SPLDV: adalah ....
S4
Penyelesaian dari SPLDV: adalah ....
S5
Penyelesaian dari SPLDV: adalah ....
S6
Penyelesaian dari SPLDV: adalah ....
S7
Penyelesaian dari SPLDV: adalah ....
S8
Penyelesaian dari SPLDV: adalah ....
S9
Penyelesaian dari SPLDV: adalah ....
S10
Tania adalah seorang konsultan di perusahaan XYZ dan digaji berdasarkan jumlah jam kerja. Jika dalam satu minggu Tania bekerja normal selama 8 jam dengan tambahan 1 jam lembur, maka ia digaji sebesar Rp730.000,00. Akan tetapi, jika dalam satu minggu Tania bekerja normal selama 6 jam dengan tambahan 3 jam lembur, maka ia digaji sebesar Rp750.000,00. Gaji Tania per jam untuk bekerja normal dan bekerja lembur berturut-turut adalah ....
