Contoh Soal Konsep Irisan Kerucut Parabola
Contoh Soal Konsep Irisan Kerucut Parabola - Suatu Kerucut jika dipotong oleh sebuah bidang datar maka akan menghasilkan beberapa kemungkinan bentuk yaitu lingkaran, parabola, elips, dan hipebola. Bentuk-bentuk ini banyak aplikasinya, misalnya fokus dari suatu hiperbola digunakan dalam long distance radio navigation system, sifat-sifat elips diaplikasikan pada lithotripter (alat penghancur batu ginjal).
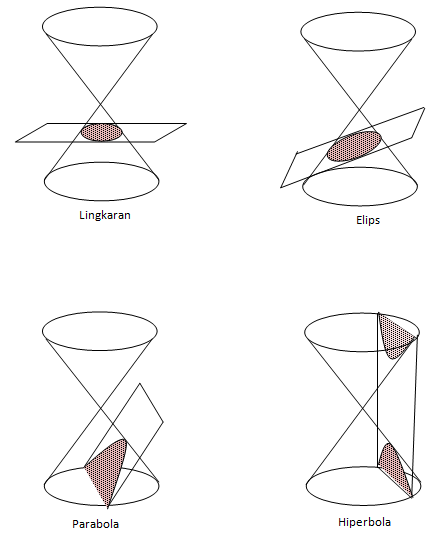
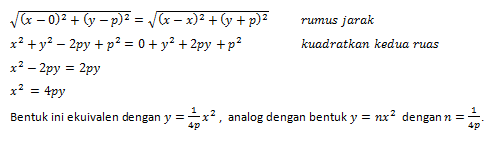
Untuk meningkatkan pemahaman kalian, mari kita cermati beberapa soal berikut ini.
Pembahasan :
Pembahasan :
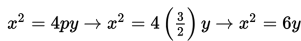

Parabola
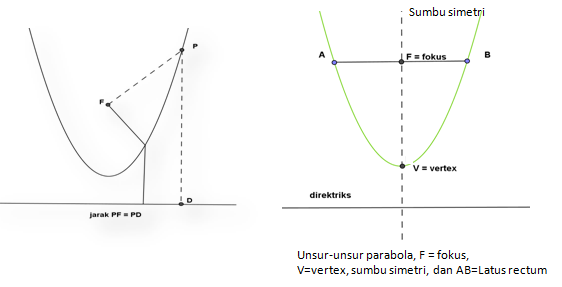
Parabola didefinisikan sebagai kumpulan titik-titik P pada suatu bidang datar yang berjarak sama dari sebuah titik F dan sebuah garis l. F adalah fokus dari parabola, dan garis l adalah direktriks dari parabola. Garis yang tegak lurus direktriks dan melalui fokus disebut sumbu simetri. Puncak (vertex) V adalah titik dimana sumbu simetri memotong parabola. Garis melalui fokus sejajar direktriks dan ujung-ujungnya pada parabola, yaitu AB disebut Latus rectum.

Mari kita perhatikan grafik parabola berikut ini!

Jarak titik P (x,y) dengan F (0,p) sama dengan jarak P (x,y) dengan D (x,-p) sehingga jarak PF = Jarak PD.
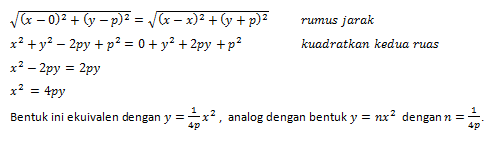
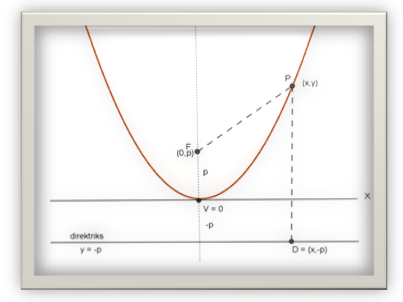
Persamaan x2 = 4py adalah bentuk sederhana dari persamaan parabola dengan
• titik puncak V (0,0)
• terbuka keatas
• sumbu Y sebagai sumbu simetri
• titik fokus terletak pada sumbu Y dengan koordinat (0,p)
• persamaan direktriks y = -p.
• terbuka keatas
• sumbu Y sebagai sumbu simetri
• titik fokus terletak pada sumbu Y dengan koordinat (0,p)
• persamaan direktriks y = -p.
Selain garis arah atau direktriks yang mendatar , kita juga mengenal garis direktriks yang tegak lurus dengan persamaan parabolanya.
Persamaan Parabola dengan puncak (a , b) dan sumbu simetri sejajar sumbu Y adalah :
(x – a)2 = 4p(y-b)
(x – a)2 = 4p(y-b)
- Koordinat puncak V (a , b)
- p negatif parabola terbuka ke bawah, p positif parabola terbuka ke atas
- Koordinat fokus F (a, b+p)
- Persamaan direktriks y = b - p
- Panjang latus rectum = 4|p|
Persamaan Parabola dengan puncak (a,b), sumbu simetri sejajar sumbu X adalah :
(y – b)2 = 4p(x – a)
(y – b)2 = 4p(x – a)
- Koordinat puncak V(a,b)
- p negatif parabola terbuka ke kiri, p positif parabola terbuka ke kanan, p≠0
- Koordinat fokus F(a+p,b)
- Persamaan direktriks X = a-p
- Panjang latus rectum = 4|p|
Untuk meningkatkan pemahaman kalian, mari kita cermati beberapa soal berikut ini.
Contoh 1 : Grafik parabola (y-2)2 = 16(x-2) terbuka kemana?
Pembahasan :
Persamaan parabola (y-2)2 = 16(x-2) artinya 4p = 16 sehingga nilai p adalah 4. nilai p positif maka parabola terbuka ke kanan.
Contoh 2 : Tentukan persamaan parabola dengan puncak (0,0) dan fokus (0,3/2)
Pembahasan :
Persamaan parabola dengan puncak (0,0) ada dua yaitu y2 = 4px atau x2 = 4py.
Karena titik fokus (0,3/2) terletak pada sumbu Y, maka sumbu simetrinya adalah sumbu Y.
Dengan demikian, persamaan parabola yang dimaksud adalah : x2 = 4py
Karena titik fokus (0,3/2) terletak pada sumbu Y, maka sumbu simetrinya adalah sumbu Y.
Dengan demikian, persamaan parabola yang dimaksud adalah : x2 = 4py
Titik fokus (0 , 3/2) = (0 , p) <=> p= 3/2
S1
Jika kerucut tegak dipotong oleh suatu bidang datar yang sejajar dengan garis pelukis dari kerucut tersebut maka akan terbentuk…
S2
Garis yang tegak lurus garis direktriks dan melalui titik fokus disebut…
S3
Suatu parabola dengan persamaan y2 = 6x, posisi sumbu simetrinya berada pada…
S4
Diketahui persamaan parabola (y-2)2 = 16(x+3), koordinat titik fokusnya adalah….
S5
Persamaan garis direktriks parabola pada soal 4 adalah…
S6
Persamaan parabola dengan puncak (0,0) dan fokus (0,5) adalah…
S7
Panjang latus rectum suatu Parabola yang memiliki persamaan (y-5)2 = 12(x-3) adalah…
S8
Jarak titik fokus suatu parabola dengan koordinat (0,6) dengan garis direktriksnya adalah…
S9
Persamaan garis direktriks parabola (x-3)2 = 12(y-4) adalah…
S10
Kurva parabola y2 - 6y - 8x + 1 = 0 akan terbuka ke..
