Contoh Soal Gerak Harmonik Sederhana
Contoh Soal Gerak Harmonik Sederhana - Gerak harmonik sederhana mengacu pada gerakan periodik (ayunan) suatu objek dari posisi setimbangnya, sehingga perpindahan maksimum pada satu sisi sama besar dengan perpindahan maksimum di sisi yang lain. Gerak ini dapat dijelaskan dan dihitung dengan menggunakan fungsi sinus dan cosinus.

Disisi lain, gaya gravitasi mendorong massa ke bawah lagi ketika mengalami tegangan terbesarnya pada titik mana perpindahan maksimum+x juga terjadi. 
.Termasuk contoh gerak ini adalah pendulum jam dan ayunan di taman bermain.

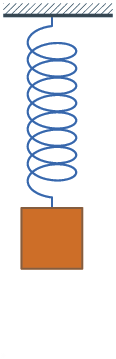
Gerak Harmonik Sederhana memiliki enam karakter. Untuk membuktikan ini, mari kita ambil contoh suatu massa yang bergetar, yang menempel pada suatu pegas vertikal (sistem massa-pegas) yang ujung lainnya dipaku ke langit-langit.
Pegas vertikal dengan konstan k, akan selalu memberi gaya (F) pada massa untuk mengembalikan massa pada posisi setimbangnya. Hukum Hooke menyatakan bahwa arah gaya pegas akan selalu berlawanan dengan arah ulur atau kompresi dari pegas.>
F= -kx
Sekarang kombinasikan persamaan ini dengan Hukum Kedua Newton, maka akan kita mendapatkan :
F = ma = -kx
Menggunakan Kalkulus, penyelesaian persamaan menjadi :
x = a cosωt
dimana:
ω = frekuensi sudut (rad/s)
F = gaya
x = perpindahan maksimum ketika fungsi cosinus sama dengan 1, atau ketika x = a
a = lebar ayunan
k = tetap
m = massa
t = waktu

Perpindahan (x):Perpindahan mengacu pada jarak dan arah suatu massa dari posisi setimbangnya.
Pegas mendorong massa ke atas ketika mengalami tegangan terberatnya, pada titik mana perpindahan maksimum −x juga terjadi.
Disisi lain, gaya gravitasi mendorong massa ke bawah lagi ketika mengalami tegangan terbesarnya pada titik mana perpindahan maksimum+x juga terjadi. 
Yang manapun itu, gaya mencapai skala terbesarnya ketika berada pada perpindahan terjauh dari posisi setimbang, dan pergerakkannya ditujukan ke arah posisi setimbang.
Kecepatan (v): Ketika massa mencapai perpindahan maksimum, massa akan berubah arah dan akan seketika berhenti bergerak. Karena itu, pada titik perpindahan maksimum, kecepatannya menjadi nol. Massa kemudian akan memperoleh kecepatannya lagi, dan bergerak ke arah yang berlawanan secara cepat melewati posisi setimbangnya, sebelum akhirnya melambat lagi karena mendekati perubahan arah selanjutnya. Kecepatan digambarkan dengan menggunakan persamaan :
v = -Aωsinωt
dimana:
v = kecepatan
A = lebar
ω = frekuensi sudut
t = waktu
S1
Tipe gerak manakah yang mengacu pada gerakan periodik suatu objek dari posisi setimbang, sehingga perpindahan maksimum di satu ujung adalah sama besar dengan perpindahan maksimum di ujung lain?
S2
Yang manakah dari pilihan berikut yang BUKAN merupakan karakter dari Gerak Harmonik Sederhana?
S3
Karakter gerakan harmonik sederhana berikut yang manakah yang mengacu pada jarak dan arah suatu objek dari posisi setimbangnya?
S4
Dalam sistem massa-pegas, kapankan massa akan berubah arah?
S5
Pada sistem massa-pegas, karakter yang manakah yang ditentukan oleh massa (m) dan kekakuan pegas, yang diekspresikan dengan istilah pegas konstan k?
S6
Contoh berikut manakah yang merupakan contoh dari sistem kekekalan?
S7
Dalam suatu sistem massa-pegas, berapakah kecepatan suatu massa ketika mencapai perpindahan maksimum?
S8
Periode getaran suatu massa sebesar 35 kg pada suatu pegas dengan konstan k = 5 N/m adalah....
S9
Suatu massa berberat 4 kg bergetar pada suatu pegas dengan konstan 8 N/m dan melewati titik setimbangnya dengan kecepatan 16 m/detik. Berapakah besar energi dari sistem massa-pegas pada titik ini?
S10
Pada sistem massa-pegas, pada titik manakah gaya yang diterapkan pada massa akan menjadi gaya yang paling besar?
