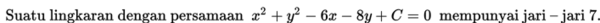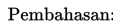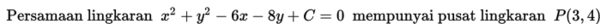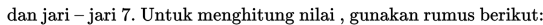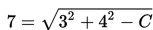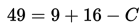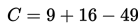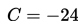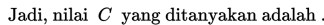Persamaan Umum Lingkaran
Persamaan Umum Lingkaran - Setelah mempelajari materi sebelumnya mengenai persamaan lingkaran, tentunya kalian telah memahami bahwa persamaan lingkaran dengan pusat P(a,b) dan berjari-jari r mempunyai persamaan baku (x - a)2 + (y - b)2 = r2. Bentuk ini mudah digunakan untuk melihat pusat dan jari-jari suatu lingkaran. Akan tetapi, tahukah kalian bahwa ada bentuk persamaan lain yang sering digunakan untuk menyatakan sebuah lingkaran? Bentuk ini berasal dari penjabaran bentuk baku.
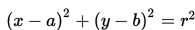
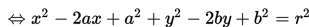
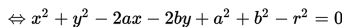
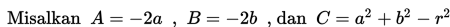
maka diperoleh bentuk umum persamaan lingkaran:
 |
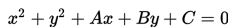
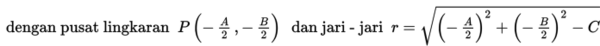
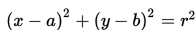
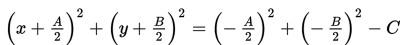
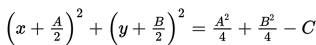
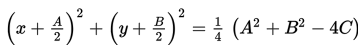
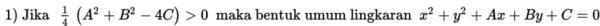
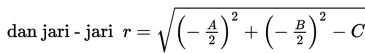
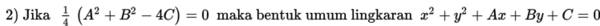
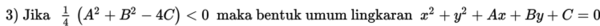
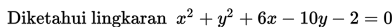
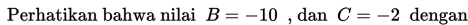
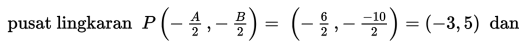
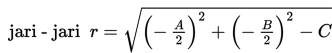
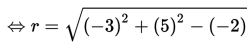
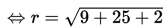
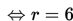
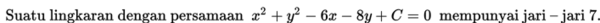
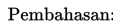
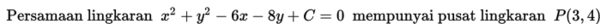
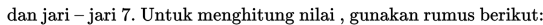
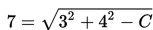
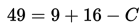
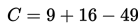
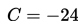
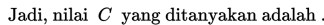
| Persamaan Umum Lingkaran |
Untuk lebih jelasnya, marilah kita jabarkan bentuk baku berikut!
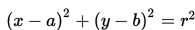
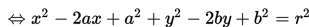
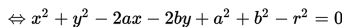
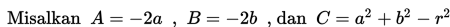
maka diperoleh bentuk umum persamaan lingkaran:
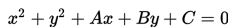
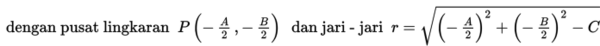
Perlu diingat bahwa tidak semua bentuk umum x2 + y2 + Ax + By + C = 0 merepresentasikan sebuah lingkaran. Jika bentuk umum lingkaran diubah ke bentuk baku maka bentuknya menjadi:
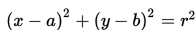
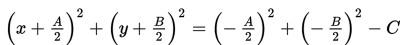
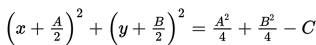
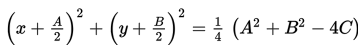
Pada persamaan dengan bentuk baku ini memiliki tiga kemungkinan.
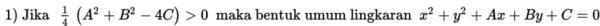
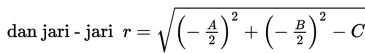
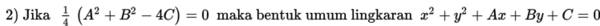
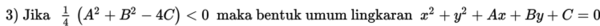
Jadi dari penjelasan di atas, dapat kita disimpulkan bahwa bentuk umum lingkaran x2 + y2 + Ax + By + C = 0 dapat merepresentasikan tiga kemungkinan yaitu sebuah lingkaran, sebuah titik, atau sebuah lingkaran imajiner.
Perhatikan contoh soal berikut!
Contoh 1
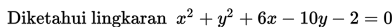
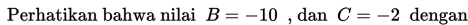
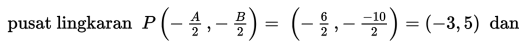
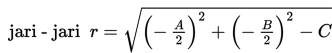
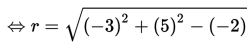
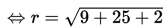
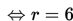
Contoh 2