Pengertian dan Rumus Arus dan Tegangan Bolak Balik

Pengertian dan Rumus Arus dan Tegangan Bolak Balik - Pada topik sebelumnya kalian telah belajar tentang timbulnya gaya gerak listrik (ggl) induksi yang disebabkan oleh perubahan fluks magnetik yang menembus suatu kumparan. Sebelum lanjut pada topik ini, ingat kembali hubungan antara besarnya ggl induksi yang timbul pada ujung-ujung kumparan dengan perubahan fluks magnetik yang dirumuskan sebagai hukum Faraday seperti pada persamaan di bawah ini.

$ε = - N \frac{d Φ}{d t}$

Keterangan:
ε = ggl induksi (V);
N = jumlah lilitan kumparan; dan

\frac{d Φ}{d t}

= laju perubahan fluks magnetik yang menembus kumparan (Wb/s).

Saat membeli lampu baru, coba kalian amati. Misalnya pada bungkus lampu yang kalian beli tertera tulisan "220 V AC, 25 W". Apa arti tulisan itu? 220 V menandakan bahwa lampu bekerja dengan baik pada tegangan arus bolak balik 220 V (tegangan PLN) dan membutuhkan daya 25 W untuk menyalakannya. Untuk mempelajari lebih lanjut tentang tegangan dan arus bolak balik, simak ulasan berikut.

A. Pengertian Arus dan Tegangan Sinusoidal

Pada topik ini bahasan dibatasi hanya pada arus dan tegangan sinusoidal sebagai salah satu contoh arus bolak-balik yang sering digunakan. Arus sinusoidal dihasilkan oleh generator arus bolak-balik atau biasa dikenal dengan dinamo. Generator arus bolak-balik terdiri dari sejumlah kumparan yang dilingkupi oleh medan magnet dimana kumparan tersebut berputar. Perusahaan listrik seperti PLN juga memanfaatkan generator yang digerakkan dengan berbagai cara. Penggerak tersebut misal air terjun atau bendungan (PLTA), tenaga diesel (PLTD), dan tenaga uap (PLTU).

Untuk menentukan besarnya ggl induksi yang dihasilkan oleh sebuah generator, perhatikan gambar di bawah ini.

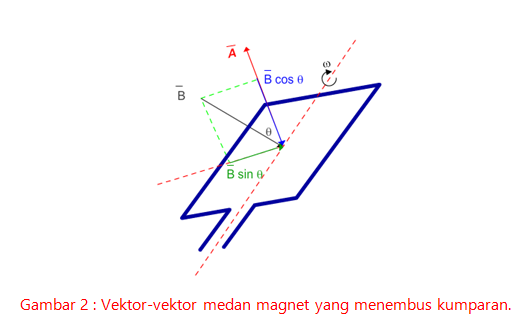
Misalkan sebuah kumparan dengan luas penampang A berputar pada porosnya dengan kecepatan sudut ω. Arah vektor luasan kumparan ditunjukkan oleh vektor Āyang tegak lurus permukaan kumparan tersebut.
Selanjunya tinjau kuat medan magnet B pada saat t yang membentuk sudut ϴterhadap vektor luasan Ā di mana ϴ = ωt. Besarnya kuat medan magnet yang menembus penampang kumparan tersebut adalah komponen vektor yang sejajar dengan kumparan, yaitu sebesar B cos ϴ. Berdasarkan hukum Faraday di atas, akan kita peroleh persamaan berikut.

$ε = - N \frac{d Φ}{d t}$

$ε = - N \frac{d (B A \cos ω t)}{d t}$

$ε = - N B A ω (- \sin ω t)$

$ε = N B A ω \sin ω t$

Keterangan:
ε = ggl induksi (V);
N = jumlah lilitan kumparan;
A = luas penampang kumparan;
B = kuat medan magnet (Wb/m2 = Tesla); dan
ω = frekuensi sudut putaran kumparan ( rad/s).

Besaran NABω pada persamaan di atas adalah harga maksimum ggl yang dihasilkan oleh generator arus bolak-balik, sehingga persamaan tersebut dapat juga ditulis sebagai berikut.

$ε = ε_{m a k s} \sin ω t$

Besaran gaya gerak listrik dapat kalian anggap identik dengan tegangan yang disimbolkan sebagai V. Dengan demikian persamaan di atas dapat ditulis sebagai berikut.

$V = V_{m a k s} \sin ω t$

Keterangan:
V = tegangan sesaat (V);
Vmaks = tegangan maksimum (V);
ω =frekuensi sudut putaran kumparan (rad/s).

Persamaan di atas merupakan persamaan tegangan arus sinusoidal. Jika sumber tegangan ini dihubungkan dengan suatu beban, maka persamaan kuat arus yang timbul pada rangkaian dapat dituliskan sebagai berikut.

$i = i_{m a k s} \sin ω t$

Keterangan:
i = kuat arus sesaat (V);
imaks = tegangan maksimum (V); dan
ω = frekuensi sudut putaran kumparan ( rad/s).

Grafik di bawah ini menunjukkan arus dan tegangan sinusoidal pada suatu saat.

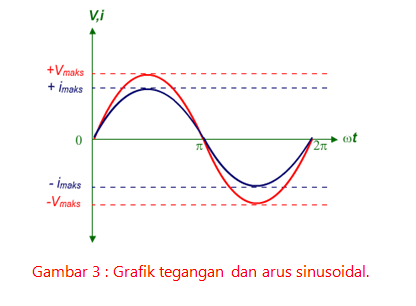
Dari pembahasan di atas dapat kita simpulkan bahwa tegangan dan arus sinusoidal adalah tegangan dan arus yang berubah secara periodik mengikuti fungsi sinus.

B. Harga Efektif dan Harga Rata-Rata Arus dan Tegangan Sinusoidal

Arus dan tegangan bolak-balik memiliki harga maksimum, harga rata-rata, dan harga efektif.

a) Harga rata-rata

Oleh karena harga sinus memiliki harga positif dan negatif yang simetris, maka untuk menentukan harga rata-rata harga fungsi ini diambil pada nilai setengah periode (π). Dengan mengintegrasi harga tegangannya, diperoleh persamaan berikut.

$V_{r} = \frac{\int_{0}^{t} V_{m a k s} \sin ω t d t}{\frac{1}{2} T}$

$V_{r} = \frac{\int_{0}^{π} V_{m a k s} \sin ω t d (ω t)}{π}$

$V_{r} = \frac{V_{m a k s}}{π} (- \cos ω t)]_{0}^{π}$

$V_{r} = - \frac{V_{m a k s}}{π} (- 1 - 1)$

$V_{r} = \frac{2 V_{m a k s}}{π}$

Vr adalah harga rata-rata tegangan bolak-balik. Dengan cara yang sama, kalian akan memperoleh harga rata-rata arusnya adalah sebagai berikut.

$i_{r} = \frac{2 i_{m a k s}}{π}$

b). Harga efektif

Pada setiap peralatan elektronik pasti akan tertera spesisfikasi tegangan dan daya yang diperlukan. Harga yang tercantum pada spesifikasi tersebut adalah harga-harga efektif tegangan yang diperlukan agar peralatan tersebut dapat bekerja dengan baik.

Misalkan pada sebuah lampu tertera 220 V, 25 W berarti alat tersebut akan bekerja dengan baik pada tegangan efektif 220 V dan akan menyerap daya 25 W. Demikian halnya ketika kalian membaca alat ukur listrik misal voltmeter atau amperemeter. Skala yang terbaca pada alat ukur tersebut merupakan harga-harga efektifnya. Untuk menenentukan harga efektif tegangan sinusouidal, gunakan persamaan di bawah ini.

${V_{e f}}^{2} = \frac{1}{2 π} \int_{0}^{2 π} {(V_{m a k s} \sin ω t)}^{2} d (ω t)$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{2 π} \int_{0}^{2 π} \frac{1}{2} (1 - \cos 2 ω t) d (ω t)$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{4 π} (\int_{0}^{2 π} d (ω t) - \int_{0}^{2 π} \cos 2 ω t d (ω t))$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{4 π} (ω t)]_{0}^{2 π} - \frac{{V_{m a k s}}^{2}}{8 π} (\sin ω t)]_{0}^{2 π}$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{4 π} (2 π - 0) - \frac{{V_{m a k s}}^{2}}{8 π} (0 - 0)$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{2}$

$V_{e f} = \frac{V_{m a k s}}{\sqrt{2}} = 0, 707 V_{m a k s}$

Dengan cara yang sama akan kalian peroleh harga efektif arusnya adalah :

$I_{e f} = \frac{I_{m a k s}}{\sqrt{2}} = 0, 707 I_{m a k s}$

C. Fasor

Pada perhitungan rangkaian arus bolak-balik, kalian akan menemui besaran-besaran vektor. Untuk menganalisis harga besaran-besaran pada rangkaian arus bolak-balik, digunakan bantuan diagram fasor. Fasor berasal dari kata fase vektor, yaitu cara menggambarkan vektor yang selalu berputar. Arah putaran fasor berlawanan dengan arah putaran jarum jam. Gambar di bawah ini adalah contoh fasor pada suatu rangkaian arus sinusoidal.

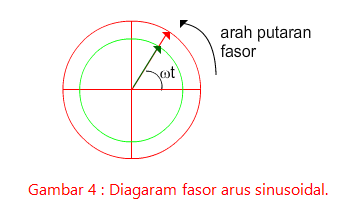
Lebih jauh tentang penggunaan fasor akan kita bahas pada topik rangkaian arus bolak-balik yang kalian pelajari pada topik berikutnya.

Contoh Soal

Seorang siswa merancang sebuah generator arus bolak-balik menggunakan kumparan sebanyak 1000 lilitan dan luas penampang 100 cm2. Kuat medan magnet yang digunakan adalah 0,5 Tesla dan generator berputar dengan frekuensi sudut 100 π rad/s. Tentukanlah ggl maksimum yang dihasilkan oleh generator tersebut.
Penyelesaian
Diketahui:
N = 1000 lilitan
A = 100 cm2 = 10-2 m2
B = 0,5 Tesla
ω = 100π rad/s
Ditanyakan: εmaks ?
Jawab:

$ε_{m a k s} = N A B ω$

$ε_{m a k s} = (1000) (10^{- 2}) (0, 05) (100 π)$

$ε_{m a k s} = 50 π V = 157 V$

Jadi, ggl maksimum yang dihasilkan generator adalah 157 V.

Pengertian dan Rumus Arus dan Tegangan Bolak Balik

ε=−NdΦdt ε=−NdΦdt

A. Pengertian Arus dan Tegangan Sinusoidal

ε=−NdΦdt ε=−NdΦdt

ε=−Nd(BAcosωt)dt ε=−Nd(BAcos⁡ωt)dt

ε=−NBAω(−sinωt) ε=−NBAω(−sin⁡ωt)

ε=NBAωsinωt ε=NBAωsin⁡ωt

ε=εmakssinωt ε=εmakssin⁡ωt

V=Vmakssinωt V=Vmakssin⁡ωt

i=imakssinωt i=imakssin⁡ωt

B. Harga Efektif dan Harga Rata-Rata Arus dan Tegangan Sinusoidal

Vr=∫0tVmakssinωtdt12T Vr=∫0tVmakssin⁡ωtdt12T

Vr=∫0πVmakssinωtd(ωt)π Vr=∫0πVmakssin⁡ωtd(ωt)π

Vr=Vmaksπ(−cosωt)]π0 Vr=Vmaksπ(−cos⁡ωt)]0π⁡

Vr=−Vmaksπ(−1−1) Vr=−Vmaksπ(−1−1)

Vr=2Vmaksπ Vr=2Vmaksπ

ir=2imaksπ ir=2imaksπ

Vef2=12π∫02π(Vmakssinωt)2d(ωt)

Vef2=12π∫02π(Vmakssin⁡ωt)2d(ωt)

Vef2=Vmaks22π∫02π12(1−cos2ωt)d(ωt)

Vef2=Vmaks22π∫02π12(1−cos⁡2ωt)d(ωt)

Vef2=Vmaks24π(∫02πd(ωt)−∫02πcos2ωtd(ωt))

Vef2=Vmaks24π(∫02πd(ωt)−∫02πcos⁡2ωtd(ωt))

Vef2=Vmaks24π(ωt)]2π0−Vmaks28π(sinωt)]2π0

Vef2=Vmaks24π(ωt)]02π−Vmaks28π(sin⁡ωt)]02π⁡

Vef2=Vmaks24π(2π−0)−Vmaks28π(0−0)

Vef2=Vmaks24π(2π−0)−Vmaks28π(0−0)

Vef2=Vmaks22 Vef2=Vmaks22

Vef=Vmaks2√=0,707Vmaks

Vef=Vmaks2=0,707Vmaks

Ief=Imaks2√=0,707Imaks Ief=Imaks2=0,707Imaks

C. Fasor

Contoh Soal

εmaks=NABω εmaks=NABω

εmaks=(1000)(10−2)(0,05)(100π)

εmaks=(1000)(10−2)(0,05)(100π)

εmaks=50πV=157V εmaks=50πV=157V

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel

$ε = - N \frac{d Φ}{d t}$

$ε = - N \frac{d Φ}{d t}$

$ε = - N \frac{d (B A \cos ω t)}{d t}$

$ε = - N B A ω (- \sin ω t)$

$ε = N B A ω \sin ω t$

$ε = ε_{m a k s} \sin ω t$

$V = V_{m a k s} \sin ω t$

$i = i_{m a k s} \sin ω t$

$V_{r} = \frac{\int_{0}^{t} V_{m a k s} \sin ω t d t}{\frac{1}{2} T}$

$V_{r} = \frac{\int_{0}^{π} V_{m a k s} \sin ω t d (ω t)}{π}$

$V_{r} = \frac{V_{m a k s}}{π} (- \cos ω t)]_{0}^{π}$

$V_{r} = - \frac{V_{m a k s}}{π} (- 1 - 1)$

$V_{r} = \frac{2 V_{m a k s}}{π}$

$i_{r} = \frac{2 i_{m a k s}}{π}$

${V_{e f}}^{2} = \frac{1}{2 π} \int_{0}^{2 π} {(V_{m a k s} \sin ω t)}^{2} d (ω t)$

${V_{e f}}^{2} = \frac{1}{2 π} \int_{0}^{2 π} {(V_{m a k s} \sin ω t)}^{2} d (ω t)$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{2 π} \int_{0}^{2 π} \frac{1}{2} (1 - \cos 2 ω t) d (ω t)$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{2 π} \int_{0}^{2 π} \frac{1}{2} (1 - \cos 2 ω t) d (ω t)$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{4 π} (\int_{0}^{2 π} d (ω t) - \int_{0}^{2 π} \cos 2 ω t d (ω t))$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{4 π} (\int_{0}^{2 π} d (ω t) - \int_{0}^{2 π} \cos 2 ω t d (ω t))$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{4 π} (ω t)]_{0}^{2 π} - \frac{{V_{m a k s}}^{2}}{8 π} (\sin ω t)]_{0}^{2 π}$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{4 π} (ω t)]_{0}^{2 π} - \frac{{V_{m a k s}}^{2}}{8 π} (\sin ω t)]_{0}^{2 π}$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{4 π} (2 π - 0) - \frac{{V_{m a k s}}^{2}}{8 π} (0 - 0)$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{4 π} (2 π - 0) - \frac{{V_{m a k s}}^{2}}{8 π} (0 - 0)$

${V_{e f}}^{2} = \frac{{V_{m a k s}}^{2}}{2}$

$V_{e f} = \frac{V_{m a k s}}{\sqrt{2}} = 0, 707 V_{m a k s}$

$V_{e f} = \frac{V_{m a k s}}{\sqrt{2}} = 0, 707 V_{m a k s}$

$I_{e f} = \frac{I_{m a k s}}{\sqrt{2}} = 0, 707 I_{m a k s}$

$ε_{m a k s} = N A B ω$

$ε_{m a k s} = (1000) (10^{- 2}) (0, 05) (100 π)$

$ε_{m a k s} = (1000) (10^{- 2}) (0, 05) (100 π)$

$ε_{m a k s} = 50 π V = 157 V$