Membandingkan Bentuk Distribusi 1
Membandingkan Bentuk Distribusi 1 - Dalam pelajaran sebelumnya, kita sudah mempelajari cara memetakan grafik dan diagram batang untuk menampilkan data secara ringkas sehingga memudahkan pembaca dalam menafsirkannya.
Namun, kita harus mampu meringkasnya sedemikian rupa sehingga ringkasan tersebut lebih cepat dan lebih mudah dipahami daripada jika tidak disajikan secara teratur.
 |
| Membandingkan Bentuk Distribusi 1 |
Namun, kita harus mampu meringkasnya sedemikian rupa sehingga ringkasan tersebut lebih cepat dan lebih mudah dipahami daripada jika tidak disajikan secara teratur.
Untuk itu, kita perlu menghitung Mean (Purata), Median (Nilai Pertengahan), dan Modus
(Nilai yang paling sering muncul) dari bermacam-macam data statistik. Selain itu, akan lebih bermanfaat, jika kita sanggup mengetahui interval dan distribusi datanya.
Mean
Mean adalah nilai rata-rata dari keseluruhan data (angka atau bilangan) dalam suatu himpunan data. Kita menghitung mean dengan menjumlahkan semua angka dalam
himpunan data dan kemudian membaginya dengan jumlah total data tersebut.
Mean = ( x1 + x2 + x3 +.......+X8) / jumlah total data
Harap diingat bahwa mean biasanya digunakan untuk menghitung nilai rata-rata dari suatu himpunan data.
Modus
Modus adalah data yang paling sering muncul dalam suatu himpunan data.
Kadang, kita perlu mencari modus himpunan data tertentu untuk menentukan popularitas suatu benda, msl.,
merek barang atau jenis olah raga, dll.
(Nilai yang paling sering muncul) dari bermacam-macam data statistik. Selain itu, akan lebih bermanfaat, jika kita sanggup mengetahui interval dan distribusi datanya.
Mean
Mean adalah nilai rata-rata dari keseluruhan data (angka atau bilangan) dalam suatu himpunan data. Kita menghitung mean dengan menjumlahkan semua angka dalam
himpunan data dan kemudian membaginya dengan jumlah total data tersebut.
Mean = ( x1 + x2 + x3 +.......+X8) / jumlah total data
Harap diingat bahwa mean biasanya digunakan untuk menghitung nilai rata-rata dari suatu himpunan data.
Modus
Modus adalah data yang paling sering muncul dalam suatu himpunan data.
Kadang, kita perlu mencari modus himpunan data tertentu untuk menentukan popularitas suatu benda, msl.,
merek barang atau jenis olah raga, dll.
MedianMedian adalah nilai pertengahan atau ukuran pemusatan dari suatu himpunan data yang terurut. Kita menghitung median dengan mengatur deretan nilai dalam urutan naik
lalu mencari nilai pertengahannya. Tetapi, jika jumlah datanya ganjil, kita dapat dengan mudah menentukan median data tersebut, yaitu dengan mencari nilai yang terletak di pertengahan data. Sebaliknya, jika jumlah datanya genap, kita mencari median dengan lebih dahulu menjumlahkan dua nilai pertengahan
lalu menghitung reratanya.
Sedangkan pada diagram batang, kita menghitung median dengan menjumlahkan seluruh deretan nilai yang ada pada diagram batang-daun lalu menghitung hingga nilai tengah dari puncak diagram batang-daun. Demikian pula, jika jumlah datanya genap, kita akan menghitung dengan
cara seperti ketika kita menghitung himpunan data sederhana.
Contoh 1
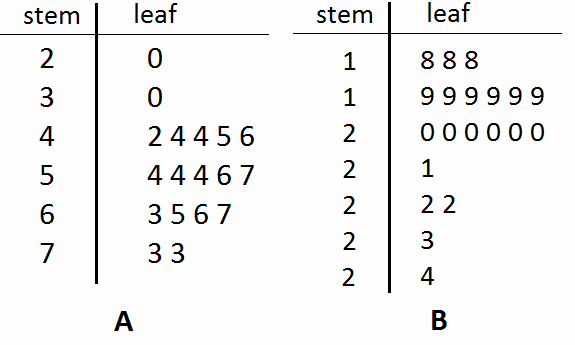
Berikut ini adalah dua diagram batang-daun. Manakah yang mempunyai median lebih besar?
lalu mencari nilai pertengahannya. Tetapi, jika jumlah datanya ganjil, kita dapat dengan mudah menentukan median data tersebut, yaitu dengan mencari nilai yang terletak di pertengahan data. Sebaliknya, jika jumlah datanya genap, kita mencari median dengan lebih dahulu menjumlahkan dua nilai pertengahan
lalu menghitung reratanya.
Sedangkan pada diagram batang, kita menghitung median dengan menjumlahkan seluruh deretan nilai yang ada pada diagram batang-daun lalu menghitung hingga nilai tengah dari puncak diagram batang-daun. Demikian pula, jika jumlah datanya genap, kita akan menghitung dengan
cara seperti ketika kita menghitung himpunan data sederhana.
Contoh 1
Berikut ini adalah dua diagram batang-daun. Manakah yang mempunyai median lebih besar?

Jawaban: A
Penjelasan
Pertama-tama, kita menghitung banyaknya data dalam diagram A.
Dalam hal ini ada 18 data. Karena jumlahnya genap, kita ambil dua nilai tengah dari deretan nilai tersebut
setelah terlebih dahulu menyusun nilai-nilai itu dalam urutan naik atau urutan turun, terserah. Dalam hal ini,
nilai tengahnya adalah 54 dan 54. Kemudian, kita hitung mean kedua nilai tengah tersebut.
Maka, mean diagram A adalah (54 + 54)/2 = 54.
Sementara itu, diagram B mempunyai 20 deretan nilai,
sehingga
mean diagram B adalah (20 + 20)/2 = 20
Dengan demikian, mean diagram A
lebih besar daripada mean diagram B.
Penjelasan
Pertama-tama, kita menghitung banyaknya data dalam diagram A.
Dalam hal ini ada 18 data. Karena jumlahnya genap, kita ambil dua nilai tengah dari deretan nilai tersebut
setelah terlebih dahulu menyusun nilai-nilai itu dalam urutan naik atau urutan turun, terserah. Dalam hal ini,
nilai tengahnya adalah 54 dan 54. Kemudian, kita hitung mean kedua nilai tengah tersebut.
Maka, mean diagram A adalah (54 + 54)/2 = 54.
Sementara itu, diagram B mempunyai 20 deretan nilai,
sehingga
mean diagram B adalah (20 + 20)/2 = 20
Dengan demikian, mean diagram A
lebih besar daripada mean diagram B.
Contoh 2
Kita mempunyai dua himpunan data sebagai berikut:
A. 12,14,13,17,5,7,8,9,13,17,10;
Kita mempunyai dua himpunan data sebagai berikut:
A. 12,14,13,17,5,7,8,9,13,17,10;

Manakah himpunan data yang mempunyai mean lebih besar?
Jawaban: B
Penjelasan
Kita menghitung mean himpunan data A
dengan menjumlahkan seluruh deretan bilangan itu lalu membaginya dengan banyaknya bilangan tersebut,
yaitu:
(12+14+13+17+5+8+9+13+17+10)/11 = 11.4
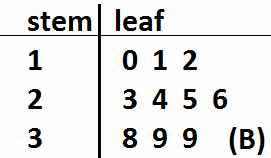
Dengan cara yang sama, kita menghitung mean diagram batang daun (Gb. B):
(10+11+12+23+24+25+26+38+39+39)/10 = 24.7
Dengan demikian, himpunan data b mempunyai mean yang lebih besar.
Jawaban: B
Penjelasan
Kita menghitung mean himpunan data A
dengan menjumlahkan seluruh deretan bilangan itu lalu membaginya dengan banyaknya bilangan tersebut,
yaitu:
(12+14+13+17+5+8+9+13+17+10)/11 = 11.4
Dengan cara yang sama, kita menghitung mean diagram batang daun (Gb. B):
(10+11+12+23+24+25+26+38+39+39)/10 = 24.7
Dengan demikian, himpunan data b mempunyai mean yang lebih besar.