Contoh Soal Deret Geometri

Contoh Soal Deret Geometri - Sama halnya dengan barisan dan deret artimetika, selain barisan geometri juga terdapat deret geometri. Seperti yang dipelajari pada materi lalu, barisan aritmetika merupakan jumlah suku-suku suatu barisan aritmetika. Apakah hubungan yang sama juga berlaku pada barisan dan deret geometri? Ayo cari tahu jawabannya dengan memahami topik ini.

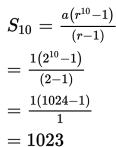
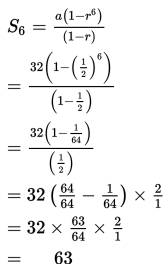
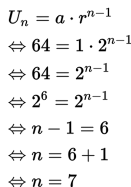
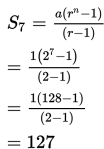
      Sebelum membahas mengenai deret geometri, ada baiknya kita mengingat kembali tentang barisan geometri. Apakah kamu masih ingat tentang barisan geometri? Pada topik sebelumnya telah dibahas bahwa suatu barisan disebut barisan geometri, jika untuk setiap bilangan asli n berlaku,

      $\frac{U_n}{U_{n-1}}=r$
Dengan, 
$U_n=a{r}^{n–1}$ = suku ke-n
$U_{n-1}$ = suku ke-(n - 1)
r = rasio atau perbandingan
a = suku pertama

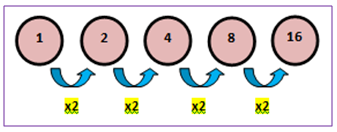
Contoh barisan geometri adalah, 1, 2, 4, 8, 16, ….Untuk lebih jelasnya, perhatikan ilustrasi berikut.

Dari ilustrasi di atas diperoleh informasi bahwa suku pertama barisan tersebut adalah a = 1 dan rasio antar sukunya adalah r = 2.

      Apa hubungan antara barisan geometri dan deret geometri? Jika $U_1,U_2,U_3,...U_n$ adalah suku-suku barisan geometri, maka $U_1+U_2+U_3+...+U_n$ disebut deret geometri. Jadi, suku-suku dari suatu deret geometri berasal dari barisan geometri. Misalnya, pada contoh di atas telah diketahui bahwa 1, 2, 4, 8, 16, … merupakan barisan geometri, maka 1 + 2 + 4 + 8 + 16 + … merupakan deret geometri. Dengan demikian diperoleh bentuk umum untuk deret geometri, yaitu:
      $a+ar+{ar}^2+{ar}^3+...$

Dengan, 
a = suku pertama
r= rasio atau perbandingan

      Seperti deret aritmetika, untuk menentukan jumlah n suku suatu deret geometri akan sangat tidak efektif apabila kita menjumlahkan suku-sukunya satu persatu. Hal ini karena membutuhkan waktu yang lebih lama dan sering terjadi kesalahan. Untuk itu, dibutuhkan cara khusus untuk menghitung jumlah n suku pertama ($S_n$) suatu deret geometri. Ada dua rumus yang digunakan untuk menghitung $S_n$ suatu deret geometri. Penggunaan rumus tersebut tergantung jenis deret geometrinya. Berikut diuraikan jenis-jenis deret geometri beserta rumus $S_n$ yang digunakan.

Deret Naik

Rumus jumlah n suku pertamanya adalah,
$S_n=\frac{a(r^n-1)}{(r-1)}$, untuk r > 1 dan r ≠ 1

Contoh Deret Naik
Deret geometri 1 + 2 + 4 + 8 + 16 + ...
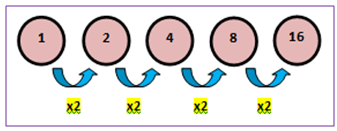
Deret tersebut disebut deret naik karena nilai suku-sukunya semakin meningkat dengan r > 1. Perhatikan ilustrasi berikut.

Dari ilustrasi diperoleh bahwa, $U_1=a$ = 1 dan $U_2$ = 2.
Sehingga, dapat dicari nilai r
$r=\frac{U_n}{U_{n-1}}=\frac{U_2}{U_1}=\frac{2}{1}$ = 2

Catatan: Kamu boleh memilih cara yang kamu anggap paling mudah untuk menentukan r, baik dengan cara ilustrasi maupun dengan rumus $r=\frac{U_n}{U_{n-1}}=\frac{U_2}{U_1}$

Oleh karena nilai r = 2 yang artinya r > 1 maka gunakan rumus $S_n$ untuk deret naik.

Misalkan kita akan menghitung jumlah 10 suku pertama ($S_{10}$) deret tersebut, maka ganti nilai a = 1, r = 2 dan n = 10 ke $S_n$. Sehingga,

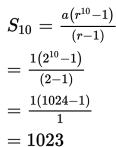
Jadi, jumlah 10 suku pertama deret tersebut adalah 1.023

Deret Turun

Rumus jumlah n suku pertamanya adalah,
$S_n=\frac{a(1-r^n)}{(1-r)}$, untuk r < 1 dan r ≠ 1

Contoh Deret Turun
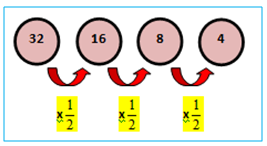
Deret geometri 32 + 16 + 8 + 4 + ...
Deret tersebut disebut deret turun karena nilai suku-sukunya semakin menurun dengan r < 1. Perhatikan ilustrasi berikut.

Dari ilustrasi diperoleh bahwa, $U_1=a$ = 32 dan $U_2$ = 16.
Sehingga, dapat dicari nilai r
$r=\frac{U_n}{U_{n-1}}=\frac{U_2}{U_1}=\frac{16}{32}=\frac{1}{2}$

Catatan: Selain menggunakan ilustrasi, nilai r juga dapat ditentukan dengan, $r=\frac{U_n}{U_{n-1}}=\frac{U_2}{U_1}=\frac{16}{32}=\frac{1}{2}$

Oleh karena nilai r = $\frac{1}{2}$ yang artinya r < 1 maka gunakan rumus $S_n$ untuk deret turun.

Misalkan kita akan menghitung jumlah 6 suku pertama ($S_6$) deret tersebut, maka ganti nilai a = 32, r = $\frac{1}{2}$ dan n = 6 ke $S_n$. Sehingga,

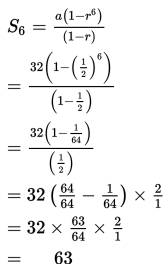
Jadi, jumlah 6 suku pertama deret tersebut adalah 63.

      Ayo pahami contoh berikut untuk menambah pengetahuanmu tentang deret geometri.

Contoh 1

Tentukan jumlah dari 1 + 2 + 4 + 8 + … + 64.

Penyelesaian
Diketahui deret geometri 1 + 2 + 4 + 8 + … + 64.
Dari deret tersebut diperoleh bahwa, $U_1=a$ = 1 dan $U_2$ = 2 dan $U_n$ = 64.

Mula-mula tentukan nilai r.
$r=\frac{U_n}{U_{n-1}}=\frac{U_2}{U_1}=\frac{2}{1}=2$

Oleh karena nilai r = 2 yang artinya r > 1 maka gunakan rumus $S_n$ untuk deret naik.

Selanjutnya, tentukan nilai n-nya, agar kita dapat menggunakan rumus $S_n=\frac{a(r^n-1)}{(r-1)}$ untuk menentukan hasil penjumlahannya.

Tentukan nilai n dengan cara,

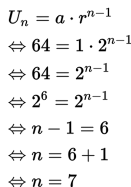
Ternyata, 64 adalah suku ke-7 ($U_7=64$ ) atau n = 7.
Tentukan hasil penjumlahan ketujuh suku pertama ($S_7$) dari 1 + 2 + 4 + 8 + … + 64 dengan mengganti nilai a = 1, r = 2 dan n = 7 ke $S_n$. Sehingga,

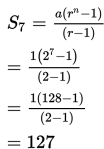
Jadi, jumlah dari 1 + 2 + 4 + 8 + … + 64 adalah 127.

S1

Pilihan Tunggal

Berikut ini yang merupakan deret geometri adalah ….

S2

Pilihan Tunggal

Suatu deret geometri dikatakan sebagai deret geometri naik, apabila ….

S3

Pilihan Tunggal

Suatu deret geometri diketahui merupakan deret geometri turun. Berikut ini pernyataan yang tepat mengenai deret tersebut adalah ….

S4

Pilihan Tunggal

Diketahui suatu deret geometri 4 + 12 + 36 + 108 + … Jumlah n suku pertama deret tersebut ditentukan dengan rumus ….

S5

Pilihan Tunggal

Jumlah 8 suku pertama deret geometri 1 + 4 + 16 + 64 + … adalah 

S6

Pilihan Tunggal

Jumlah 6 suku pertama deret geometri : 16 + 8 + 4 + 2 + … adalah ….

S7

Pilihan Tunggal

Jumlah n suku pertama suatu deret geometri ditentukan oleh rumus $S_n=2^{n+1}-2$. Suku pertama deret tersebut adalah ….

S8

Pilihan Tunggal

Jumlah n suku pertama suatu deret geometri ditentukan oleh rumus $S_n=3.2^n-3$. Rasio deret tersebut adalah ….

S9

Pilihan Tunggal

Jumlah n suku pertama suatu deret geometri ditentukan oleh rumus $S_n=\frac{5^n-1}{4}$. Suku ke-3 deret tersebut adalah ....

S10

Pilihan Tunggal

Diketahui suku pertama dan suku ke-3 suatu deret geometri adalah 6 dan 24. Jumlah 4 suku pertama deret geometri tersebut adalah ….

Share this post