Contoh Soal Rata-Rata

Contoh Soal Rata-Rata - Mari kita ingat kembali tentang data yang telah dibahas di topik sebelumnya. Data merupakan kumpulan informasi yang dapat diolah dan disajikan agar mendapatkan keterangan yang diinginkan. Salah satu hasil pengolahan data yang dapat kita hitung adalah ukuran pemusatan data. Ukuran pemusatan data menggambarkan suatu nilai yang mewakili keseluruhan data. Ada 3 macam ukuran pemusatan data yaitu mean (rata-rata), median (nilai tengah), dan modus (nilai yang sering muncul). Pada topik ini kita akan membahas mengenai ukuran pemusatan data yaitu rata-rata.

Rata-Rata (Mean)

Rata-rata merupakan salah satu ukuran pemusatan data yang dihitung dengan membagi jumlah seluruh data dengan banyak data. Rata-rata juga disebut dengan rataan dan dilambangkan dengan $\overline{x}$. Ada beberapa macam jenis rata-rata berdasarkan datanya yaitu rata-rata data tunggal, rata-rata data berfrekuensi, dan rata-rata gabungan.

Rata-Rata Data Tunggal

Data tunggal adalah data yang disajikan dalam bentuk uraian sederhana tanpa tabel.

Misalnya diketahui berat badan anggota suatu keluarga adalah sebagai berikut.

Berat badan ayah = 67 kg
Berat badan ibu = 52 kg
Berat badan kakak = 56 kg
Berat badanku = 45 kg
Berat badan adek = 30 kg

Berdasarkan pengertiannya, rata-rata dihitung dengan membagi jumlah seluruh data dengan banyak data.

Jumlah data diperoleh dari menjumlahkan berat badan seluruh anggota keluarga, sedangkan banyak data diperoleh dari banyak anggota keluarga.

Ini berarti, rata-rata berat badan keluarga tersebut adalah:

$\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{a}-\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{a}\left(\overline{x}\right)=\frac{\mathrm{J}\mathrm{u}\mathrm{m}\mathrm{l}\mathrm{a}\mathrm{h}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}{\mathrm{B}\mathrm{a}\mathrm{n}\mathrm{y}\mathrm{a}\mathrm{k}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}$

$\iff \overline{x}=\frac{67+52+56+45+30}{5}$

$\iff \overline{x}=\frac{250}{5}$

$\iff \overline{x}=50$

Jadi rata-rata berat badan pada keluarga tersebut adalah 50 kg.

Berdasarkan uraian di atas, rata-rata data tunggal dapat ditentukan dengan rumus:

$\mathrm{R}\mathrm{a}\mathrm{t}\mathrm{a}-\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{a}\left(\overline{x}\right)=\frac{\mathrm{J}\mathrm{u}\mathrm{m}\mathrm{l}\mathrm{a}\mathrm{h}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}{\mathrm{B}\mathrm{a}\mathrm{n}\mathrm{y}\mathrm{a}\mathrm{k}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{a}}=\frac{x_1+x_2+x_3+...+x_n}{n}$

dengan:
xn = datum ke-n
n = banyak data

Rata-Rata Data Berfrekuensi

Apakah kamu masih ingat tentang tabel distribusi frekuensi? Sebuah data dapat disajikan dalam tabel distribusi frekuensi seperti di bawah ini.

dengan:
x1 = datum ke-1
x2 = datum ke-2
x3 = datum ke-3
⁞ 
xi = datum ke-i
f1 = frekuensi untuk x1
f2 = frekuensi untuk x2
f3 = frekuensi untuk x3
⁞
fi = frekuensi untuk xi

Pada tabel distribusi frekuensi, data yang sama tidak dituliskan berualang-ulang, tetapi dituliskan frekuensinya.

Rata-rata untuk data berfrekuensi adalah:

$\overline{x}=\frac{f_1{x}_1+f_2{x}_2+f_3{x}_3+...+f_n{x}_n}{f_1+f_2+f_3+...+f_n}$

Rata-Rata Gabungan

Jika terdapat beberapa kelompok data yang masing-masing rata-ratanya diketahui, maka kita dapat menenetukan rata-rata gabungan dari kelompok-kelompok data tersebut.

Misalnya:
kelompok data ke-1 memiliki rata-rata x1
kelompok data ke-2 memiliki rata-rata x2 
kelompok data ke-3 memiliki rata-rata x3
⁞
kelompok data ke-i memiliki rata-rata xi

Rata-rata gabungan kelompok data tersebut adalah:

$\overline{x}=\frac{n_1{\overline{x}}_1+n_2{\overline{x}}_2+n_3{\overline{x}}_3+...+n_i{\overline{x}}_i}{n_1+n_2+n_3+...+n_i}$

dengan:
$\overline{x}$ = rata-rata gabungan
n1 = banyak data kelompok 1
n2 = banyak data kelompok 2
n3 = banyak data kelompok 3
⁞
ni = banyak data kelompok ke-i

Agar kamu lebih paham, mari simak contoh-contoh soal berikut.

◙ ◙ ◙ Contoh 1 ◙ ◙ ◙

Diketahui berat badan dari 10 siswa kelas 9 (dalam kg) adalah:
56, 60, 72, 40, 45, 47, 50, 41, 42, 42.
Tentukan rata-rata berat badan dari 10 anak tersebut.

Penyelesaian:

Jadi, rata-rata berat badan kesepuluh anak tersebut adalah 49,5 kg.

S1

Diketahui nilai uian akhir Matematika di kelas IX B sebagai berikut.
10, 7, 8, 6, 6, 10, 9, 7, 8, 10
5, 4, 3, 5, 6, 9, 10, 10, 6, 7
Rata-rata nilai Ujian Akhir Matematika tersebut adalah ....

S2

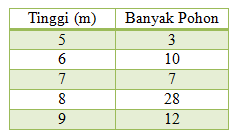
Saat melakukan pengamatan tinggi pohon di hutan jati, tim peneliti memperoleh data tinggi pohon sebagai berikut.

Rata-rata tinggi pohon di kawasan hutan jati tersebut adalah....

S3

Diketahui data nilai ulangan Matematika 15 siswa sebagai berikut : 
7 5 4 6 5 7 8 6 4 4 5 9 5 6 4
Banyak siswa yang nilainya di atas rata–rata adalah ....

S4

Rata-rata berat badan siswa adalah 54,5 kg, sedangkan rata-rata berat badan siswi adalah 45 kg. Jika banyak siswa adalah 24 orang dan siswi adalah 16 orang, maka rata-rata berat badan keseluruhannya adalah ... kg.

S5

Rata–rata nilai ulangan Matematika 14 siswa di suatu sekolah adalah 7,0. Seorang siswa bernama Yogi mengikuti ulangan susulan karena saat ulangan berlangsung ia sedang sakit. Jika nilai Yogi ditambahkan, maka nilai rata–rata siswa berubah menjadi 6,8. Nilai Yogi pada tes tersebut adalah ....

S6

Upah rata–rata tiga orang karyawan adalah Rp423.000,00 per bulan. Setelah satu karyawan baru masuk, upah rata–rata turun menjadi Rp373.500,00 per bulan. Upah karyawan baru tersebut adalah ....

S7

Rata-rata nilai 30 siswa adalah 7,4. Setelah nilai 2 siswa yang ikut ulangan susulan digabungkan, rata-rata nilainya menjadi 7,5. Rata-rata nilai kedua siswa tersebut adalah ....

S8

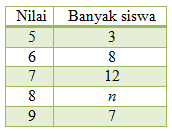
Tabel di bawah ini menyatakan nilai ulangan harian Matematika siswa kelas IX.

Jika diketahui rata-rata nilai ulangan harian matematika tersebut adalah 7,25, maka banyak siswa yang mendapatkan nilai 8 adalah ....

S9

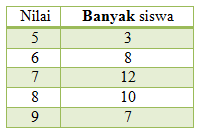
Tabel di bawah ini menyatakan nilai ulangan harian Matematika. Banyak siswa yang mendapat nilai kurang dari nilai rata-rata adalah ....

S10

Nilai rata-rata Matematika dalam suatu kelas 72. Rata-rata nilai siswa adalah 69 dan rata-rata nilai siswi adalah 74. Jika banyak seluruh anggota kelas adalah 40 orang, maka banyak siswa adalah ....

Share this post