Contoh Soal Rumus Jumlah dan Selisih Tangen
Contoh Soal Rumus Jumlah dan Selisih Tangen - Untuk mendapatkan rumus jumlah tangen, kita harus menentukan bentuk yang bersesuaian dengan pernyataan tan α + tan β. Seperti yang kita ketahui, untuk sebarang sudut x fungsi tangen dapat didefinisikan sebagai:
Oleh karena itu, pernyataan yang bersesuaian dengan tan α + tan β dapat kita tentukan dengan langkah sebagai berikut.
Ingat kembali bahwa, sin (α + β) = sin α cos β + cos α sin β, sehingga baris terakhir persamaan di atas dapat kita tulis sebagai:
Bentuk ini sudah cukup sederhana dan sudah dapat digunakan dalam perhitungan, namun kita masih dapat melakukan sedikit pengembangan dengan memperhatikan bahwa 2 cos α cos β = cos (α + β) + cos (α - β), sehingga kita peroleh:
Jadi, rumus jumlah tangen adalah sebagai berikut.
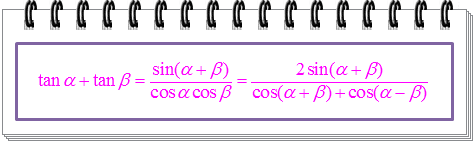
Ingat kembali bahwa, sin (α - β) = sin α cos β - cos α sin β, sehingga baris terakhir persamaan di atas dapat kita tulis sebagai:
Perhatikan bahwa 2 cos α cos β = cos (α + β) + cos (α - β), sehingga persamaan di atas dapat kita tuliskan menjadi:
Jadi, rumus selisih tangen adalah:
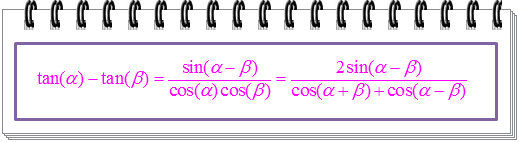
Oleh karena itu, pernyataan yang bersesuaian dengan tan α + tan β dapat kita tentukan dengan langkah sebagai berikut.
Ingat kembali bahwa, sin (α + β) = sin α cos β + cos α sin β, sehingga baris terakhir persamaan di atas dapat kita tulis sebagai:
Bentuk ini sudah cukup sederhana dan sudah dapat digunakan dalam perhitungan, namun kita masih dapat melakukan sedikit pengembangan dengan memperhatikan bahwa 2 cos α cos β = cos (α + β) + cos (α - β), sehingga kita peroleh:
Jadi, rumus jumlah tangen adalah sebagai berikut.
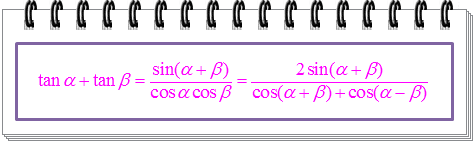
🔢 Rumus Selisih Tangen
Selanjutnya, untuk mendapatkan rumus selisih tangen, kita harus menentukan bentuk yang bersesuaian dengan pernyataan tan α - tan β. Dengan prinsip yang sama dengan sebelumnya, pernyataan yang bersesuaian dengan tan α - tan β dapat kita tentukan sebagai berikut.
Ingat kembali bahwa, sin (α - β) = sin α cos β - cos α sin β, sehingga baris terakhir persamaan di atas dapat kita tulis sebagai:
Perhatikan bahwa 2 cos α cos β = cos (α + β) + cos (α - β), sehingga persamaan di atas dapat kita tuliskan menjadi:
Jadi, rumus selisih tangen adalah:
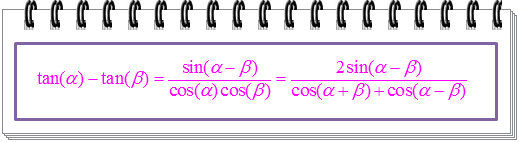
SOAL 1
Nilai dari tan 75° + tan 15° adalah….
SOAL 2
Nilai dari tan 97,5° + tan 37,5° adalah …
SOAL 3
Nilai dari tan 37,5° + tan 82,5° adalah ….
SOAL 4
Bentuk lain dari tan 4x + tan 2x berdasarkan rumus jumlah tangen adalah …
SOAL 5
Nilai dari tan 37,5° - tan 7,5° adalah ….
SOAL 6
Nilai dari tan 142,5° - tan 7,5° adalah ….
SOAL 7
Nilai dari tan 45° - tan 225° adalah …
SOAL 8
Bentuk lain dari tan 9y - tan 3y berdasarkan rumus selisih tangen adalah ….
SOAL 9
Jika a merupakan sudut pada kuadran pertama, maka bentuk yang setara dengan tan a - tan 2a adalah ….
SOAL 10
Jika diketahui dan dengan α, β sudut di kuadran pertama, maka nilai dari tan α + tan β adalah ....
