Contoh Soal Hubungan antara direktriks, titik fokus, dan titik-titik pada Ellips
Contoh Soal Hubungan antara direktriks, titik fokus, dan titik-titik pada Ellips - Setelah kalian mempelajari cara menggambar Ellips, mari kita ingat kembali beberapa unsur ellips, agar kalian dapat menentukan hubungan antara komponen-komponen ellips dengan persamaaan ellips.
Persamaan Ellips dengan pusat (0,0)
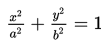
Keterangan :
Sedangkan
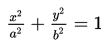
II. Persamaan Elips dengan Pusat (α,β)
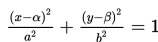
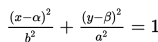
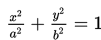
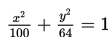
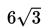
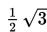
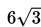
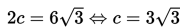
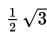
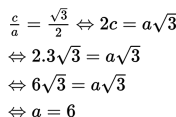
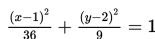
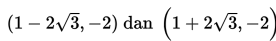
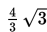
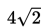
Persamaan Ellips dengan pusat (0,0)
Bentuk umum persamaan Ellips adalah :
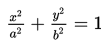

a2 = b2 + c2
Keterangan :
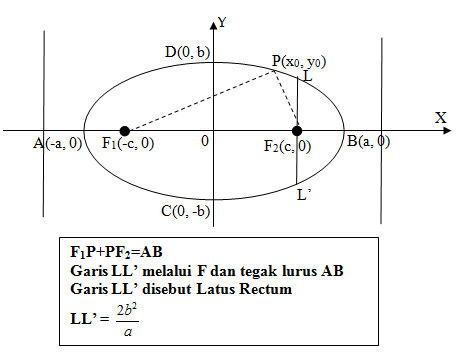
- Pusatnya adalah titik O(0,0).
- Fokusnya adalah titik F1(-c,0) dan F2(c,0)
- Sumbu X adalah sumbu mayor dan dan sumbu Y adalah sumbu minor jika a > b.
- Persamaan sumbu mayor adalah y = 0 dan persamaan sumbu minor adalah x = 0.
- Ellips akan memotong sumbu X di titik A(-a,0) dan B(a,0) dan memotong sumbu Y di titik C(0, -b) dan D(0,b). Keempat titik itu masing-masing disebut puncak ellips.
- AB = 2a disebut sumbu-panjang atau sumbu mayor dan CD = 2b disebut sumbu pendek atau sumbu minor.
- Persamaan Direktriks : x = ± a2 + c
- Eksentrisitas : e = c/a
Sedangkan
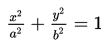
: merupakan persamaan elips dengan pusat O(0,0) yang sumbu panjangnya 2b dan sejajar sumbu Y sedang sumbu pendeknya 2a dan sejajar sumbu X.
II. Persamaan Elips dengan Pusat (α,β)
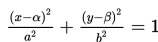
Keterangan:
1. Pusat (α,β)
2. Puncak A1(α + a, β) dan A2(α - a, β)
3. Fokus F1(α + c, β) dan F2(α - c, β)
4. Sumbu simetri x = α dan y = β
5. Sumbu panjang = 2a dan sumbu pendek = 2b
6. Persamaan direktriks : x = ± a2 /c + α
7. Eksentrisitas : e = c/a
1. Pusat (α,β)
2. Puncak A1(α + a, β) dan A2(α - a, β)
3. Fokus F1(α + c, β) dan F2(α - c, β)
4. Sumbu simetri x = α dan y = β
5. Sumbu panjang = 2a dan sumbu pendek = 2b
6. Persamaan direktriks : x = ± a2 /c + α
7. Eksentrisitas : e = c/a
Sedangkan :
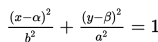
merupakan persamaan elips dengan pusat (α,β) yang sumbu panjangnya 2b dan sejajar sumbu Y sedang sumbu pendeknya 2a dan sejajar sumbu X.
Contoh :
1. Sebuah ellips yang mempunyai pusat (0,0) mempunyai persamaan direktris x = 25/2 dan eksentrisitas : e = 4/5. Tentukan persamaan ellips tersebut!
1. Sebuah ellips yang mempunyai pusat (0,0) mempunyai persamaan direktris x = 25/2 dan eksentrisitas : e = 4/5. Tentukan persamaan ellips tersebut!
Jawab :
Dari persamaan direktris : x = 25/2
-> a2 /c = 25/2
<=> 2a2 = 25c ............(1)
Dari persamaan direktris : x = 25/2
-> a2 /c = 25/2
<=> 2a2 = 25c ............(1)
Dari eksentrisitas: ((1+1)/2,(0+4)/2)
-> c/a = 4/5
<=> 4a = 5c .................(2)
-> c/a = 4/5
<=> 4a = 5c .................(2)
Substitusi persamaan (2) ke persamaan (1) diperoleh
2a2 = 25 c
2a2 = 5.5c
2a2 = 5.4a
2a2 = 20a
2a2 – 20a = 0
2a(a – 10) = 0
2a = 0 atau a = 10
Jadi a = 10 diperoleh 5c = 40 , sehingga c = 8 ,
b2 = a2 – c2
<=> b2 = 100 - 64
<=> b = 8
2a2 = 25 c
2a2 = 5.5c
2a2 = 5.4a
2a2 = 20a
2a2 – 20a = 0
2a(a – 10) = 0
2a = 0 atau a = 10
Jadi a = 10 diperoleh 5c = 40 , sehingga c = 8 ,
b2 = a2 – c2
<=> b2 = 100 - 64
<=> b = 8
Substitusikan nilai a = 10 dan b = 8 ke persamaan ellips:
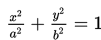
sehingga diperoleh persamaan ellips:
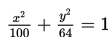
- Suatu ellips mempunyai jarak antara kedua fokus =
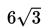
dan eksentrisitas =
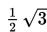
jika pusat ellips tersebut adalah (1, 2). Tentukan persamaan ellips tersebut!
Jawab :
Fokus =
Jawab :
Fokus =
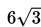
artinya
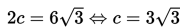
eksentrisitas=
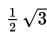
berarti
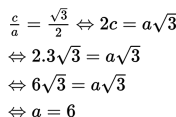
b2 = a2 – c2 = 36 – 27 = 9 sehingga b = 3
Persamaan ellips dengan a = 6 , b = 3 dan pusat (1, 2) adalah
Persamaan ellips dengan a = 6 , b = 3 dan pusat (1, 2) adalah
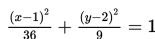
S1
Koordinat pusat suatu Ellips adalah (0,0), jika ellips tersebut mempunyai panjang sumbu mayor 8 dan sumbu minor 4, maka persamaan ellips tersebut adalah ….
S2
Sebuah persamaan ellips mempunyai koordinat puncak sumbu mayor
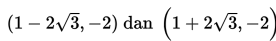
, koordinat ujung sumbu minornya adalah (1, 0) dan (1, - 4). Persamaan ellips tersebut adalah ….
S3
Sebuah Ellips yang berpusat di (0, 0) mempunyai panjang sumbu mayor 10 dan panjang sumbu minor = 8. Persamaan ellips tersebut adalah ….
S4
Salah satu persamaan direktris dari suatu ellips dengan pusat (- 2 , 4) adalah x = 17/4, sedangkan eksentrisitasnya e = 4/5. Persamaan ellips tersebut adalah ….
S5
Sebuah ellips mempunyai pusat (1, -2), panjang Latus Rectum =
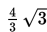
serta jarak dua titik fokusnya =
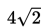
. Eksentrisitas dari persamaan ellips tersebut adalah .…
S6
Sebuah ellips yang dengan pusat (1, 2) mempunyai dua fokus yang berjarak 6 dan eksentrisitas = 0,6. Persamaan ellips tersebut adalah ….
S7
Koordinat titik-titik fokus sebuah ellips adalah (17, -1) dan (-13, -1). Jika eksentrisitas ellips tersebut adalah 15/17, maka persamaan ellips tersebut …
S8
Persamaan di bawah ini yang merupakan persamaan ellips adalah ….
S9
Sebuah ellips mempunyai puncak dengan koordinat (15, 2), ujung sumbu minor berkoordinat (5, 8) dan direktris tegak lurus sumbu x. Persamaan direktris ellips tersebut adalah ….
S10
Sebuah taman berbentuk ellips. Panjang sumbu mayor dan minornya secara berturut-turut adalah 200 meter dan 160 meter. Pengelola taman tersebut ingin menambahkan lampu taman pada masing-masing fokus. Jarak antara kedua lampu taman adalah ….
