Konsep Dasar Matriks dalam Persamaan Linear

Konsep Dasar Matriks dalam Persamaan Linear -  Sebelumnya kalian telah mempelajari cara menyelesaikan sistem persamaan linear dua variabel maupun tiga variabel menggunakan cara eliminasi, substitusi, maupun gabungan eliminasi dan substitusi.

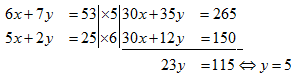
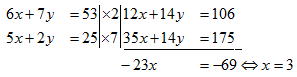
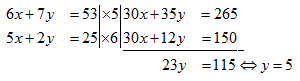
Apakah ada di antara kalian yang lupa?

Mari kita pelajari kembali cara menyelesaikan sistem persamaan linear dengan cara eliminasi maupun gabungan antara eliminasi dengan substitusi agar nantinya kalian dapat menggunakannya sebagai rujukan dalam memeriksa hasil penyelesaian sistem persamaan linear.

Contoh 1:

Tentukan himpunan penyelesaian dari sistem persamaan linear dua variabel:

{6x+7y=535x+2y=25  $\{\begin{array}{c}6x+7y=53\\ 5x+2y=25\end{array}$

dengan menggunakan cara eliminasi.

Penyelesaian:

Eliminasi variabel x:

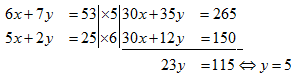
Eliminasi variabel y:

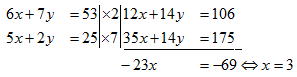
Jadi, himpunan penyelesaian adalah {(3,5)}.

Contoh 2:

Tentukan himpunan penyelesaian dari sistem persamaan linear dua variabel:

{6x+7y=535x+2y=25  $\{\begin{array}{c}6x+7y=53\\ 5x+2y=25\end{array}$

dengan menggunakan cara gabungan eliminasi dan substitusi.

Penyelesaian:

Eliminasi variabel x:

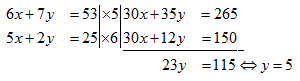
Selanjutnya dengan mensubtitusikan nilai variabel y ke persamaan kedua, diperoleh hasil sebagai berikut:

5x+2y=25⇔5x+2(5)=25⇔5x+10=25⇔5x=15⇔x=3  $\begin{array}{l}5x+2y=25\\ \iff 5x+2\left(5\right)=25\\ \iff 5x+10=25\\ \iff 5x=15\\ \iff x=3\end{array}$

Jadi, himpunan penyelesaian adalah {(3,5)}.

Jika kalian perhatikan, hasil akhir dari contoh soal 1 dan 2 adalah sama.

Menyelesaikan Sistem Persamaan Linear Dua Variabel

Bagaimanakah cara menyelesaikan sistem persamaan linear dua variabel dengan menggunakan matriks?

Ada dua langkah yang perlu kalian ikuti, yaitu:

• mengubah sistem persamaan linear ke dalam bentuk persamaan matriks
• menentukan nilai variabel dengan menggunakan metode invers matriks

Mari kita ingat kembali cara menentukan invers matriks persegi berordo 2 x 2.

Jika diketahui 
A=(acbd ) $A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$, maka invers matriks A adalah [% {{A}{-1}}=\frac{1}{ad-bc}\left(

d−c−ba $$\begin{array}{cc}d& -b\\ -c& a\end{array}$$

\right)\ %], dengan syarat ad−bc≠0 $ad-bc\ne 0$.

Contoh 3:

Tentukan himpunan penyelesaian sistem persamaan linear: {5x+2y=243x−y =10  $\{\begin{array}{c}5x+2y=24\\ 3x-y=10\end{array}$

dengan menggunakan metode invers matriks.

Penyelesaian:

Langkah I

Bentuk persamaan matriks dari sistem persamaan linear dalam contoh soal adalah (532−1 )(xy )=(2410 ) $\left(\begin{array}{cc}5& 2\\ 3& -1\end{array}\right)\left(\begin{array}{c}x\\ y\end{array}\right)=\left(\begin{array}{c}24\\ 10\end{array}\right)$

Langkah II

Berdasarkan metode invers matriks: AX = B ⇔ X = A-1B, maka kita peroleh hasil sebagai berikut:

Berdasarkan uraian di atas, dapat disimpulkan bahwa himpunan penyelesaian dari sistem persamaan dalam contoh soal adalah {(4, 2}.

Menyatakan Sistem Persamaan Linear Tiga Variabel Dalam Bentuk Matriks

Tahukah kalian bahwa sistem persamaan linear tiga variabel juga dapat dinyatakan dalam bentuk persamaan matriks?

Mari kita perhatikan contoh berikut ini.

Contoh 4:

Tulislah sistem persamaan linear:

⎧⎩⎨⎪⎪x+2y+3z2x−3y+z3x+y+2z===6117  $\{\begin{array}{lll}x+2y+3z& =& 6\\ 2x-3y+z& =& 11\\ 3x+y+2z& =& 7\end{array}$

dalam bentuk matriks.

Penyelesaian:

Oleh karena sistem persamaan linear dalam contoh soal akan dibawa ke dalam bentuk persamaan AX = B, maka bentuk persamaan matriksnya adalah ⎛⎝⎜⎜1232−31312 ⎞⎠⎟⎟⎛⎝⎜⎜xyz ⎞⎠⎟⎟=⎛⎝⎜⎜6117 ⎞⎠⎟⎟ 

Tag : rumus matriks, contoh soal matriks, matriks invers, perkalian matriks, matriks singular, contoh soal persamaan matriks, determinan matriks, transpose matriks

Share this post