Teorema Fundamental Kalkulus I

Teorema Fundamental Kalkulus I - Apakah kalian pernah mendengar teorema fundamental kalkulus?

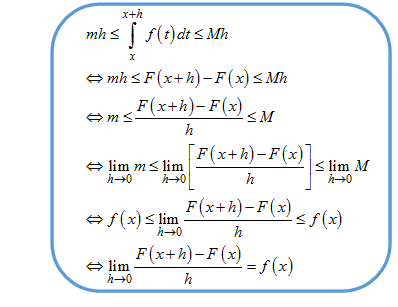
Teorema fundamental kalkulus ada dua. Nah, pada topik kali ini, kalian akan belajar mengenai teorema fundamental kalkulus I.

Yuk kita cermati dua ilustrasi berikut untuk mendapatkan gambaran tentang teorema fundamental kalkulus I.

Ilustrasi

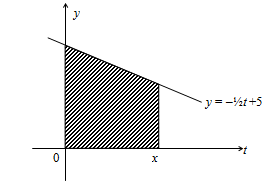
★$★$ Ilustrasi I

Diberikan suatu daerah yang dibatasi oleh garis y=−12t+5$y=-\frac{1}{2}t+5$, dimana 0≤t≤x$0\le t\le x$.

Dengan menggunakan rumus trapesium, kita ketahui bahwa luas daerah yang diarsir pada gambar di atas adalah

A(x)===12(−12x+5+5)x12(−12x+10)x−14x2+5x$\begin{array}{lll}A\left(x\right)& =& \frac{1}{2}\left(-\frac{1}{2}x+5+5\right)x\\ & =& \frac{1}{2}\left(-\frac{1}{2}x+10\right)x\\ & =& -\frac{1}{4}{x}^2+5x\end{array}$

Turunan dari A(x)$A(x)$ adalah sebagai berikut:

A′(x)===dAdxddx(−14x2+5x)−12x+5$\begin{array}{lll}{A}^{\prime }\left(x\right)& =& \frac{dA}{dx}\\ & =& \frac{d}{dx}\left(-\frac{1}{4}{x}^2+5x\right)\\ & =& -\frac{1}{2}x+5\end{array}$

Berdasarkan konsep jumlah Riemann, maka luas daerah yang diarsir pada gambar di atas dapat dinyatakan dalam bentuk A(x)=∫0x(−12t+5)dt$A\left(x\right)=\underset{0}{\overset{x}{\int }}\left(-\frac{1}{2}t+5\right)dt$.

Nah, dari uraian di atas, dapat kita simpulkan bahwa A′(x)=ddx∫0x(−12t+5)dt=−12x+5$A^{\prime }\left(x\right)=\frac{d}{dx}\underset{0}{\overset{x}{\int }}\left(-\frac{1}{2}t+5\right)dt=-\frac{1}{2}x+5$.

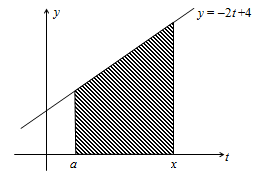
★$★$ Ilustrasi II

Diberikan suatu daerah yang dibatasi oleh garis y=−2t+4$y=-2t+4$, dimana a≤t≤x$a\le t\le x$.

Dengan menggunakan rumus trapesium, kita ketahui bahwa luas daerah yang diarsir pada gambar di atas adalah

A(x)===12(−2a+4−2x+4)(x−a)12(−2(x+a)+8)(x−a)−(x2−a2)+4(x−a)$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{lll}A\left(x\right)& =& \frac{1}{2}\left(-2a+4-2x+4\right)\left(x-a\right)\\ & =& \frac{1}{2}\left(-2\left(x+a\right)+8\right)\left(x-a\right)\\ & =& -\left(x^2-a^2\right)+4\left(x-a\right)\end{array}$

Turunan dari A(x)$A(x)$ adalah sebagai berikut:

A′(x)===dAdxddx(−(x2−a2)+4(x−a))−2x+4$\begin{array}{lll}{A}^{\prime }\left(x\right)& =& \frac{dA}{dx}\\ & =& \frac{d}{dx}\left(-\left(x^2-a^2\right)+4\left(x-a\right)\right)\\ & =& -2x+4\end{array}$

Berdasarkan konsep jumlah Riemann, maka luas daerah yang diarsir pada gambar di atas dapat dinyatakan dalam bentuk A(x)=∫ax(−2t+4)dt$A\left(x\right)=\underset{a}{\overset{x}{\int }}\left(-2t+4\right)dt$.

Nah, dari uraian di atas, dapat kita simpulkan bahwa A′(x)=ddx∫ax(−2t+4)dt=−2x+4$A^{\prime }\left(x\right)=\frac{d}{dx}\underset{a}{\overset{x}{\int }}\left(-2t+4\right)dt=-2x+4$.

Teorema Fundamental Kalkulus I

Berdasarkan kedua ilustrasi di atas, apa yang dapat kalian simpulkan?

Kesimpulan dari dua ilustrasi di atas merupakan isi dari teorema fundamental kalkulus I.

Jika fungsi f$f$ kontinu pada interval [a,b]$[a,b]$ dan x$x$ adalah sebarang titik pada interval (a,b)$(a,b)$, maka ddx∫axf(t)dt=f(x)$\frac{d}{dx}\underset{a}{\overset{x}{\int }}f\left(t\right)dt=f\left(x\right)$.

Yuk kita buktikan teorema tersebut.

Jika dimisalkan F(x)=∫axf(t)dt$F\left(x\right)=\underset{a}{\overset{x}{\int }}f\left(t\right)dt$, maka

F(x+h)=∫ax+hf(t)dt⇔F(x+h)=∫axf(t)dt+∫xx+hf(t)dt⇔F(x+h)=F(x)+∫xx+hf(t)dt⇔F(x+h)−F(x)=∫xx+hf(t)dt$\begin{array}{l}\mathrm{<br>}\end{array}$

$\begin{array}{l}F\left(x+h\right)=\underset{a}{\overset{x+h}{\int }}f\left(t\right)dt\\ \iff F\left(x+h\right)=\underset{a}{\overset{x}{\int }}f\left(t\right)dt+\underset{x}{\overset{x+h}{\int }}f\left(t\right)dt\\ \iff F\left(x+h\right)=F\left(x\right)+\underset{x}{\overset{x+h}{\int }}f\left(t\right)dt\end{array}$

$\begin{array}{l}\\ \iff F\left(x+h\right)-F\left(x\right)=\underset{x}{\overset{x+h}{\int }}f\left(t\right)dt\end{array}$

Selanjutnya, jika kita misalkan

• nilai minimum f(x)$f(x)$ untuk x$x$ pada interval [a, b] adalah m$m$
• nilai maksimum f(x)$f(x)$ untuk x$x$ di [a, b] adalah M$M$

maka kita peroleh hubungan sebagai berikut:

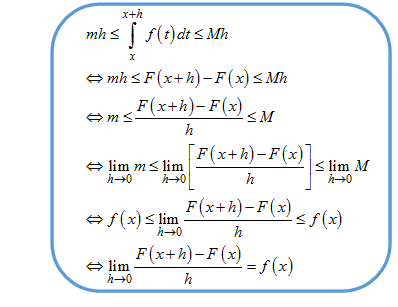
Selanjutnya, karena limh→0F(x+h)−F(x)h=ddxF(x)=ddx∫axf(t)dt$\underset{h\to 0}{lim}\frac{F\left(x+h\right)-F\left(x\right)}{h}=\frac{d}{dx}F\left(x\right)=\frac{d}{dx}\underset{a}{\overset{x}{\int }}f\left(t\right)dt$, maka terbukti bahwa ddx∫axf(t)dt=f(x)$\frac{d}{dx}\underset{a}{\overset{x}{\int }}f\left(t\right)dt=f\left(x\right)$.

Teorema fundamental kalkulus I mudah dipahami bukan?

Share this post